2023 - 実装改良編 #
概要 #
前ページでは,
\[2023=(2+0+2+3)(2^2+0^2+2^2+3^2)^2\]であることに着目して,以下の問題を解いたのでした.
Problem 1. 整数 \(x=\sum_{j=0}^{n-1}a_j10^j\) \((0\le a_j\le 9,j=0,1,\dots,n-1)\) に対して, \[ \prod_{k=1}^K\sum_{j=0}^{n-1}a_j^{i_k}=x \] を満たす整数 \(K\ge1\), \(1\le i_1\le\cdots\le i_K\) が存在するかを判定せよ.存在する場合はこの方程式を満たす \((i_1,i_2,\dots,i_K)\) をひとつ求めよ.
本ページでは,そこで解説した解法を改良する方法を説明します. その後,改良前後で実行時間を比較します.ただし,結果はほとんど変わりませんでした.
実装改良 #
前ページで解説した解法は以下のとおりでした1.
Algorithm 2. \(\mathtt{Solve}(a, x, i)\) の擬似コードを以下で定める.ただし,\((a_1,\dots,a_n)\in\mathbb{N}^n,(b_1,\dots,b_m)\in\mathbb{N}^m\) に対して,\(\mathtt{append}(a,b)=(a_1,\dots,a_n,b_1,\dots,b_m)\in\mathbb{N}^{n+m}\) とする.
- Input: \(a\in\mathbb{N}^n,x\in\mathbb{N},i\in\mathbb{N}\)
- Output: \(\prod_{k=1}^K\sum_{j=0}^{n-1}a_j^{i_k}=x,i\le i_1\le\dots\le i_K\) を満たす \((i_1,i_2,\dots,i_K)\)
- if \(\max(a)\le1\) then
- if \(i>1\) then return \(\emptyset\)
- if \(\sum_{j=0}^{n-1}a_j=x\) then return \((1)\)
- else return \(\emptyset\)
- end if
- for \(i’=i,i+1,\dots\) do
- \(y\leftarrow\sum_{j=0}^{n-1}a_j^{i’}\)
- if \(y>x\) then return \(\emptyset\)
- if \(y=x\) then return \((i’)\)
- if \(y\mid x\) then
- \(L\leftarrow\mathtt{Solve}(a,x/y,i’)\)
- if \(L=\emptyset\) then return \(\emptyset\)
- else return \(\mathtt{append}((i’),L)\)
- end if
- end for
このアルゴリズムは,11行目によって再帰処理になっていますが, 再帰させずに,単に \(x\) を \(x/y\) に置き換えて処理を継続させることができます. この場合,再帰処理用に用意していた第3引数の \(i\) が不要になります.
これをもとに,改良したアルゴリズムは以下のとおりです.
Algorithm 3. \(\mathtt{Solve}(a, x)\) の擬似コードを以下で定める.ただし,\((a_1,\dots,a_n)\in\mathbb{N}^n,(b_1,\dots,b_m)\in\mathbb{N}^m\) に対して,\(\mathtt{append}(a,b)=(a_1,\dots,a_n,b_1,\dots,b_m)\in\mathbb{N}^{n+m}\) とする.
- Input: \(a\in\mathbb{N}^n,x\in\mathbb{N}\)
- Output: \(\prod_{k=1}^K\sum_{j=0}^{n-1}a_j^{i_k}=x,1\le i_1\le\dots\le i_K\) を満たす \((i_1,i_2,\dots,i_K)\)
- if \(\max(a)\le1\) then
- if \(\sum_{j=0}^{n-1}a_j=x\) then return \((1)\)
- else return \(\emptyset\)
- end if
- \(i\leftarrow 1\)
- loop
- \(y\leftarrow\sum_{j=0}^{n-1}a_j^i\)
- if \(y>x\) then return \(\emptyset\)
- if \(y=x\) then return \(\mathtt{append}(L,(i))\)
- if \(y\mid x\) then
- \(L\leftarrow\mathtt{append}(L,(i))\)
- \(x\leftarrow x/y\)
- else
- \(i\leftarrow i+1\)
- end if
- end loop
再帰処理がなくなりました.
さらにいえば,前ページの実装では,
\((i_1,i_2,\dots,i_K)\)
の表現に numpy.ndarray を使っていましたが,配列に動的に要素を追加していく必要があるので,list を用いた方が高速に処理できることが期待されます.
これらをもとに改良した実装は下記のとおりです.
実行時間の比較 #
改良前後で実行時間を比較した結果は,以下の Figure 1. のとおりです.計算機環境は Intel(R) Core(TM) i7-9700 CPU @ 3.00GHz x8, Linux OS (Ubuntu 22.04.1 LTS), メモリ 16.0GB, Python 3.10.6, NumPy 1.24.1 です.
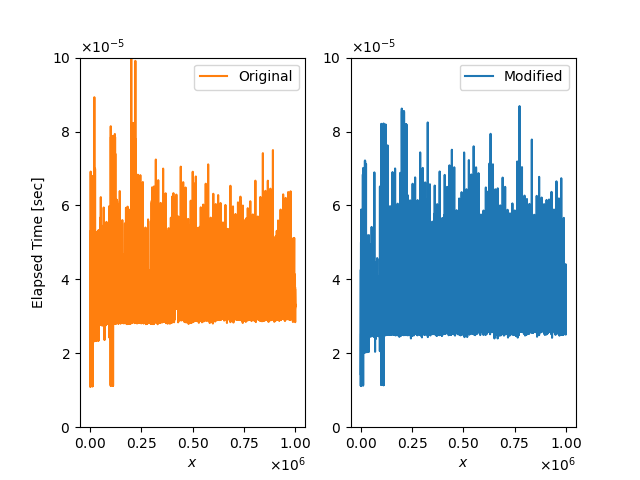
Figure 1. 改良前(左)と改良後(右)の実行時間の比較
計測対象は,整数 \(x\) から10進数表示したときの各桁 \((a_j)\) を取り出す操作を含めた処理で, \(0\le x<10^6\) について計測しました.各 \(x\) について,この処理を1回ずつ5回計測し,最大値・最小値を除いた3回の平均値をプロットしています.これは,1回あたり \(10^{-5}\) 秒という非常に短い実行時間に対して,何らかの原因により,稀に処理に \(10^{-3}\) 秒程度かかることがあるためです.各 \(x\) について, \(10^5\) 回続けて実行する前後で処理時間を計測し, \(10^5\) で割った値を結果とするなど方法もありますが,ここでは簡易な方法で求めました.
Figure 1. の左右の図から,改良後のほうがやや実行時間が短くなっているようにもみえますが,もともと \(10^{-5}\) 秒程度で求まっていることもあり,ほとんど差は見られませんでした.
また, \(x\) によらず,ほとんど実行時間がかわらないこともわかります.
まとめ #
本ページでは,前ページの \(2023=(2+0+2+3)(2^2+0^2+2^2+3^2)^2\) に関する問題を解くための実装を改良する方法を説明しました.
改良後のほうがやや実行時間が短くなっているようにもみえますが,もともと \(10^{-5}\) 秒程度で求まっていることもあり,ほとんど差は見られませんでした.
\(A\mid B\) とは, \(A\) が \(B\) を割り切るという意味です. ↩︎