ラプラス分布や切断ラプラス分布からのサンプリング

ラプラス分布や切断ラプラス分布からのサンプリング #

概要 #

ラプラス分布と切断ラプラス分布 のページでは，ラプラス分布と切断ラプラス分布の定義を述べ，切断ラプラス分布の確率密度関数，累積分布関数を具体的に求めました．

本ページでは，ラプラス分布や切断ラプラス分布からのサンプリングの方法について述べます．

逆関数法 #

指定した分布に従う乱数をサンプリングする方法として，逆関数法 と呼ばれる方法が知られています．

ラプラス分布や切断ラプラス分布に従う乱数を，この方法で生成することを考えます．まずは，逆関数法についてまとめます． 本節の議論は，ラプラス分布や切断ラプラス分布に限らず適用できます．

\(X\) を確率変数とし， \(F_X\) を \(X\) の累積分布関数とします． \(F_X\) は単調増加関数です． \(F_X^*:[0,1]\to\mathbb{R}\) を， \(F_X^*(u)=\inf\{x\mid F(x)\ge u\}\) とします1． ここで， \(U\) を区間 \([0,1]\) 上の一様分布とします． つまり， \[ f_U(u)=\begin{cases} 1,& 0\le u\le 1,\\ 0,&\text{otherwise} \end{cases} \] とします． \(Z=F_X^*(U)\) とすると， \[ \begin{aligned} F_Z(z)&=P([Z\le z])\\ &=P([F^*_X(U)\le z])\\ \end{aligned} \] となりますが， \(F^*_X(u)\le z\) であることと \(u\le F_X(z)\) であることは同じことなので， \[ \begin{aligned} F_Z(z)&=P([F^*_X(U)\le z])\\ &=P([U\le F_X(z)])\\ &=F_U(F_X(z))\\ &=F_X(z) \end{aligned} \] となり， \(Z\) の累積分布関数は \(X\) の累積分布関数に一致します．

したがって， \(u\) を区間 \([0,1]\) 上の一様分布に従う乱数とし， \(x=F_X^*(u)\) と変換すると， \(X\) の従う分布からのサンプリングができることになります． 特に， \(F_X\) が可逆であれば， \(F_X^*=F_X^{-1}\) なので， \(x=F_X^{-1}(u)\) と計算できます．

ラプラス分布からのサンプリング #

本節では，逆関数法を用いた，ラプラス分布からのサンプリング方法について述べます．

前ページ にあわせて， \(Y\) をパラメータ \(\mu,b\) のラプラス分布に従う確率変数とします． 逆関数法でラプラス分布からのサンプリングを行うには， \(Y\) の累積分布関数 \(F_Y\) の逆関数 \(F_Y^{-1}\) を求める必要があります． ここで， \(F_Y\) は狭義単調増加関数であることに注意してください．

ラプラス分布に従う確率変数の累積分布関数は，前ページ で述べたとおり， \[ F_Y(y;\mu,b)=\begin{cases} \dfrac{1}{2}\exp\left(-\dfrac{|y-\mu|}{b}\right),&y<\mu,\\ 1-\dfrac{1}{2}\exp\left(-\dfrac{|y-\mu|}{b}\right),&y\ge\mu \end{cases} \] となります．

\(0\le u\le 1/2\) とします． \(y<\mu\) において， \[ \frac{1}{2}\exp\left(-\dfrac{|y-\mu|}{b}\right)=u \] を満たす \(y\) を求めると， \[ |y-\mu|=-b\log 2u \] となりますが， \(y<\mu\) なので， \[ y=\mu+b\log 2u \] となります．

次に， \(1/2 とします． \(y\ge\mu\) において， \[ 1-\frac{1}{2}\exp\left(-\frac{|y-\mu|}{b}\right)=u \] を満たす \(y\) を求めると， \[ |y-\mu|=-b\log 2(1-u) \] となりますが， \(y\ge\mu\) なので， \[ y=\mu-b\log 2(1-u) \] となります．

よって，

\[ y=\begin{cases} \mu+b\log 2u,&0\le u\le1/2,\\ \mu-b\log 2(1-u),&1/2 < u\le1 \end{cases} \]

となります．

ここで， \(w=u-1/2\) とすると，

\[ y=\begin{cases} \mu+b\log(1+2w),&-1/2\le w\le0,\\ \mu-b\log(1-2w),&0 < w\le1/2 \end{cases} \]

となるので，

\[ \mathrm{sgn}(w)=\begin{cases} +1,\quad w\ge0,\\ -1,\quad w<0 \end{cases} \]

とすると，

\[ \begin{aligned} y&=\mu-\mathrm{sgn}(w)b\log(1-2\mathrm{sgn}(w)w)\\ &=\mu-\mathrm{sgn}(w)b\log(1-2|w|)\\ \end{aligned} \]

と書けます． ここで， \(\mathrm{sgn}(w)w=|w|\) を使いました．

したがって，次が成り立ちます．

Proposition 1. \(\mu,b\in\mathbb{R}\), \(b>0\) とする．\(W\) を区間 \([-1/2,1/2]\) 上の一様分布に従う連続的確率変数とすると，\(Y=\mu-\mathrm{sgn}(W)b\log(1-2|W|)\) は，パラメータ \(\mu,b\) のラプラス分布に従う連続的確率変数である．

切断ラプラス分布からのサンプリング #

前節と同様に，切断ラプラス分布からのサンプリングの方法を導きます．

ラプラス分布に従う確率変数の累積分布関数は，前ページ で述べたとおり，

\[ \begin{aligned} &F_X(x;\mu,b,A,B)\\ &=\begin{cases} 0,&x < A,\\ \dfrac{F_Y(x;\mu,b)-F_Y(A;\mu,b)}{C_{\mu,b}(A,B)},&A\le x\le B\\ 1,&x > B \end{cases} \end{aligned} \]

となります．

まず， \(x < A\) ならば \(F_X(x;\mu,b,A,B)=0\) なので， \(F_X^*(0)=-\infty\) です． 次に， \(x>B\) ならば \(F_X(x;\mu,b,A,B)=1\) なので， \(F_X^*(1)=B\) です．

ここで， \(0 < u < 1\) とし， \(F_X(x;\mu,b,A,B)=u\) となる \(x\) を求めます． まず， \[ \frac{F_Y(x;\mu,b)-F_Y(A;\mu,b)}{C_{\mu,b}(A,B)}=u \] なので， \[ F_Y(x;\mu,b)=uC_{\mu,b}(A,B)+F_Y(A;\mu,b) \] です．したがって， \(w=uC_{\mu,b}(A,B)+F_Y(A;\mu,b)-1/2\) とおくと， \[ x=\mu-\mathrm{sgn}(w)b\log(1-2|w|) \] となります．ここで，

\[ F_Y(A;\mu,b)-\frac{1}{2} < w < C_{\mu,b}(A,B)+F_Y(A;\mu,b)-\frac{1}{2}=F_Y(B;\mu,b)-\frac{1}{2} \] です．

さて， \(w=F_Y(A;\mu,b)-1/2,F_Y(B;\mu,b)-1/2\) であるとき，それぞれ \(x=A,B\) であることがわかります2．

そこで， \(F_X^*(0)=A\) と定義し直すと3，以下の結論が得られます．

Proposition 2. \(\mu,b\in\mathbb{R}\), \(b>0\), \(A,B\in\mathbb{R}\), \(A\le B\) とする．\(W\) を区間 \([F_Y(A;\mu,b)-1/2,F_Y(B;\mu,b)-1/2]\) 上の一様分布に従う連続的確率変数とすると，\(Y=\mu-\mathrm{sgn}(W)b\log(1-2|W|)\) は，パラメータ \(\mu,b,A,B\) の切断ラプラス分布に従う連続的確率変数である．

数値例 #

実際に切断ラプラス分布に従う乱数を生成してみます． サンプリング数 \(N=100000\) で，相対度数によるヒストグラムを作成します．

その結果は以下のとおりで，各パラメータにしたがった分布をなしていることがわかります． 例えば，

  • Figs. 1–4 では，区間 \([A,B]\) で分布が切断されていることがわかります．
  • Figs. 1, 2 を比較すると，切断点は変わらないまま，Fig. 2の方が値がばらついていることがわかります．これは，Fig. 2の方が，パラメータ \(b\) の値が大きいからです．

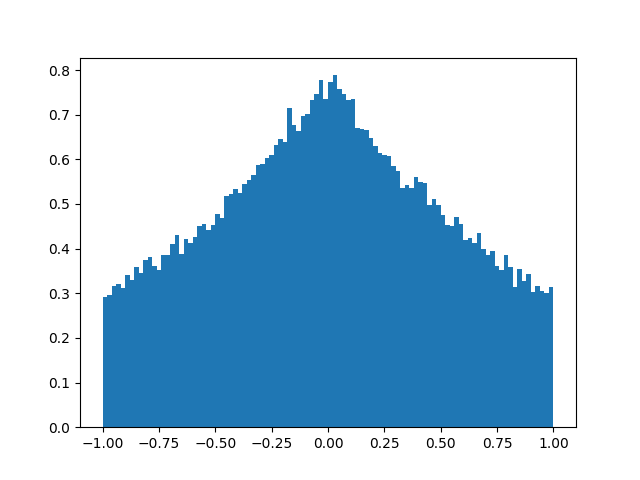
Figure 1. \(\mu=0, b=1, A=-1, B=1\)のヒストグラム

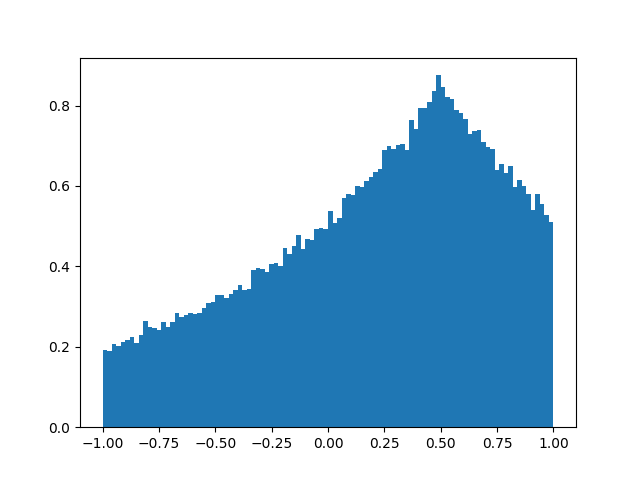
Figure 2. \(\mu=0.5, b=1, A=-1, B=1\)のヒストグラム

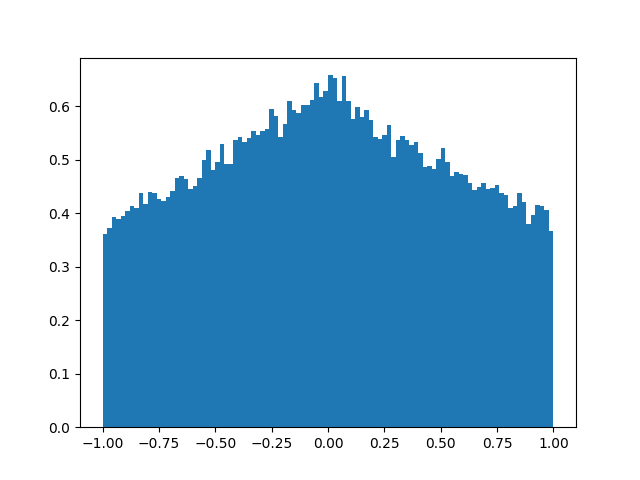
Figure 3. \(\mu=0, b=2, A=-1, B=1\)のヒストグラム

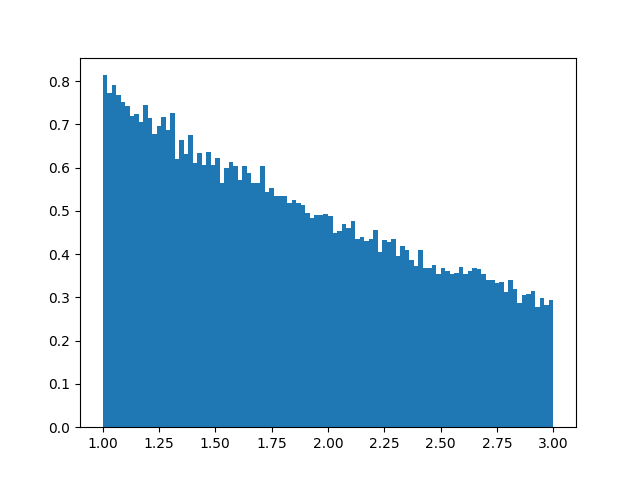
Figure 4. \(\mu=0.5, b=2, A=1, B=3\)のヒストグラム

また，本数値実験は，以下の実装で行いました．

import numpy as np
import scipy.stats as stats

def trunclap(loc=0.0, scale=1.0, low=-1.0, high=1.0, size=None):
    uniform_low = stats.laplace.cdf(low, loc, scale) - 1/2
    uniform_high = stats.laplace.cdf(high, loc, scale) - 1/2
    w = np.random.default_rng().uniform(low=uniform_low, high=uniform_high, size=size)
    r = loc - np.sign(w) * scale * np.log(1 - 2*np.abs(w))
    return r

なお，ヒストグラムは以下の方法で作成しています．

import matplotlib.pyplot as plt

def hist(random_values):
    plt.hist(random_values, bins=100, density=True)
    plt.show()

まとめ #

本ページでは，ラプラス分布や切断ラプラス分布からのサンプリングの方法についてまとめました． 切断ラプラス分布に従う乱数も，通常のラプラス分布に従う乱数と同様に，ある区間上の一様乱数を変換することで得られることがわかりました．

数値例では，実際に切断ラプラス分布に従う乱数が生成できることを確認しましたが，目視での確認はできるものの，実際に指定したパラメータで乱数生成ができているかまで確認できませんでした． \(A,B,\mu\) はよいですが， \(b\) が困難です． 次ページでは，その部分的な解決策を与えます．

参考文献 #

[1] Wikipedia，“逆関数法 - Wikipedia”, https://ja.wikipedia.org/wiki/%E9%80%86%E9%96%A2%E6%95%B0%E6%B3%95, 2024/6/5 最終アクセス．

  1. [1] で述べられている定め方です． ↩︎

  2. 前者は \(A<\mu,A\ge\mu\) で場合分けして整理すると得られます．後者も同様です． ↩︎

  3. \(F_X^*(0)=-\infty\) として， \(Z=F_X^*(U)\) としてつくる確率変数 \(Z\) と， \(F_X^*(0)=A\) として， \(Z'=F_X^*(U)\) としてつくる確率変数 \(Z'\) は，ほとんど至るところ等しいので，本質的な違いはありません． ↩︎

This work is licensed under CC BY 4.0

January 19, 2025