特殊なラプラス分布や切断ラプラス分布のパラメータ推定 #
概要 #
前ページ では,ラプラス分布や切断ラプラス分布からのサンプリングについてまとめました.
本ページでは,ラプラス分布や切断ラプラス分布に従う乱数から,各分布のパラメータを推定する方法についてまとめます.
ただし,本節は,簡易な直接計算でラプラス分布の性質を述べることを目的としているので,すべてのパラメータでなく,一部のパラメータのみを推定する場合を考えます.
具体的には, \(\mu\) は \(0\) に固定し,切断ラプラス分布では左右対称な分布となるケースのみを考えます.
\(\mu=0\) であるラプラス分布のパラメータ推定 #
いま, \(X_1,X_2,\dots,X_N\) を,独立にパラメータ \(\mu,b\) のラプラス分布に従う確率変数とし, \(\mu=0\) とします.
このとき, \[ f_{X_1,X_2,\dots,X_N}(x_1,x_2,\dots,x_N;b)=\prod_{i=1}^N\frac{1}{2b}\exp\left(-\frac{|x_i|}{b}\right) \] と表されます. \(\mathcal{L}_{x_1,\dots,x_N}(b)=\log f_{X_1,X_2,\dots,X_N}(x_1,x_2,\dots,x_N;b)\) とおくと, \[ \begin{aligned} \mathcal{L}_{x_1,\dots,x_N}(b)&=\log\prod_{i=1}^N\frac{1}{2b}\exp\left(-\frac{|x_i|}{b}\right)\\ &=\sum_{i=1}^N\left(\log\frac{1}{2b}+\log\exp\left(-\frac{|x_i|}{b}\right)\right)\\ &=-N\log 2b-\frac{1}{b}\sum_{i=1}^N|x_i| \end{aligned} \] となります.
ここで, \(\mathcal{L}_{x_1,\dots,x_N}(b)\) が最大となるような \(b\) を求めます. \[ \begin{aligned} \frac{d\mathcal{L}_{x_1,\dots,x_N}}{db}(b)&=-\frac{N}{b}+\frac{1}{b^2}\sum_{i=1}^N|x_i|\\ &=-\frac{N}{b^2}\left(b-\frac{1}{N}\sum_{i=1}^N|x_i|\right),\\ \frac{d^2\mathcal{L}_{x_1,\dots,x_N}}{db^2}(b)&=\frac{N}{b^2}-\frac{2}{b^3}\sum_{i=1}^N|x_i|\\ &=\frac{N}{b^3}\left(b-\frac{2}{N}\sum_{i=1}^N|x_i|\right) \end{aligned} \] なので, \(b=(1/N)\sum_{i=1}^N|x_i|\) とすると, \(d\mathcal{L}_{x_1,\dots,x_N}/db=0\) , \(d^2\mathcal{L}_{x_1,\dots,x_N}/db^2=-(1/b^3)\sum_{i=1}^N|x_i|<0\) なので, \(b=(1/N)\sum_{i=1}^N|x_i|\) で \(\mathcal{L}_{x_1,\dots,x_N}(b)\) は最大値をとります.
よって, \(x_1,x_2,\dots,x_N\) がパラメータ \(\mu,b\) のラプラス分布からサンプリングされた乱数であって, \(\mu=0\) が既知であれば, \(b=(1/N)\sum_{i=1}^N|x_i|\) と推定することができます.
このように,対数尤度関数 \(\mathcal{L}_{x_1,\dots,x_N}(b)\) を最大化してパラメータを推定する方法を,最尤推定 といいます1.
\(\mu=0\) である対称な切断ラプラス分布のパラメータ推定 #
いま, \(X_1,X_2,\dots,X_N\) を,独立に同一の分布に従う確率変数とし,その確率密度関数が, \[ \begin{aligned} &f_{X_i}(x;b,A)=\begin{cases} \dfrac{1}{2bC_{b}(A)}\exp\left(-\dfrac{|x|}{b}\right),&-A\le x\le A,\\ 0,&\text{otherwise}, \end{cases},\\ &C_{b}(A)=1-\exp\left(-\dfrac{A}{b}\right) \end{aligned} \] であるとします. これは,切断ラプラス分布の特殊な場合ものです.
前節と同様に, \(\mathcal{L}_{x_1,\dots,x_N}(b,A)=\log f_{X_1,X_2,\dots,X_N}(x_1,x_2,\dots,x_N;b,A)\) とおくと, \[ \begin{aligned} \mathcal{L}_{x_1,\dots,x_N}(b,A)&=\log\prod_{i=1}^N\frac{1}{2bC_b(A)}\exp\left(-\frac{|x_i|}{b}\right)\\ &=\sum_{i=1}^N\left(\log\frac{1}{2bC_b(A)}+\log\exp\left(-\frac{|x_i|}{b}\right)\right)\\ &=-N\log 2bC_b(A)-\frac{1}{b}\sum_{i=1}^N|x_i| \end{aligned} \] となります.
まず, \(b>0\) とすると, \(A\to0\) のとき \(\mathcal{L}_{x_1,\dots,x_N}(b,A)\to+\infty\) なので, \(A\) は小さければ小さいほどよいです. 一方で,すべての \(i\) について \(|x_i|\le A\) となる必要があるため, \(A=\max_{i=1,2,\dots,N}|x_i|\) と推定することにします.
次に, \(b\) について考えます. 偏導関数に着目すると,
\[ \begin{aligned} &\frac{\partial\mathcal{L}_{x_1,\dots,x_N}}{\partial b}(b,A)\\ &\quad=-\frac{N}{b^2}\left(b-\frac{A}{\exp(A/b)-1}-\frac{1}{N}\sum_{i=1}^N|x_i|\right),\\ \end{aligned} \] となります.
ここで,
- \(b\to+0\) において, \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)\to+\infty\)
- \(b\to+\infty\) において, \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)\to+0\)
であることがわかります.
さらに, \(b-(1/N)\sum_{i=1}^N|x_i|\) は \(b\) に関する1次関数, \(A/(\exp(A/b)-1)\) は \(b\) に関する狭義凸関数なので,これら関数のグラフは高々2点で交わります.よって, \(b\) に関する方程式 \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)=0\) は高々2個の実数解をもちます.
\(b\approx0\) において \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)>0\) で, \(b\) が十分大きい範囲で \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)>0\) なので,偏導関数の連続性から,次のいずれかが成り立ちます.
- 常に \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)\ge0\) である,
- \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)=0\) は異なる2個の実数解をもち,小さい方の解 \(b^*\) は, \((\partial\mathcal{L}_{x_1,\dots,x_N}/\partial b)(b,A)\) が正から負に変化する零点である.
さらに, \(b\to+\infty\) のとき, \(\mathcal{L}_{x_1,\dots,x_N}(b,A)\to-N\log 2A\) であることに注意すると, \(b^*\) が存在し,かつ \(\mathcal{L}_{x_1,\dots,x_N}(b^*,A)\ge-N\log 2A\) のとき \(b^*\) をパラメータ \(b\) の推定値とできることがわかります.
ただし,解くべき以下の方程式は,一般に解析的に解けないので,数値的に解く必要があります. \[ b=\frac{A}{\exp(A/b)-1}+\frac{1}{N}\sum_{i=1}^N|x_i| \]
なお, \[ \begin{aligned} &\frac{\partial^2\mathcal{L}_{x_1,\dots,x_N}}{\partial b^2}(b,A)\\ &\quad=\frac{N}{b^4}\left(\frac{A^2\exp(A/b)}{(\exp(A/b)-1)^2}-\frac{2Ab}{\exp(A/b)-1}+b\left(b-\frac{2}{N}\sum_{i=1}^N|x_i|\right)\right) \end{aligned} \] と表せることを利用して,数値的に得られた \(b^*\) が極大点であることを確認することができます.
数値実験 #
実際に切断ラプラス分布に従う乱数を生成し,本ページの方法でパラメータ推定を行います.
条件は以下のとおりとします.
- サンプリング数 \(N=100000\) とします.
- 乱数生成は前ページの方法で行います.
- \(b\) に関する方程式は,初期値を \(1\) , 収束判定条件を残差の絶対値が \(10^{-15}\) 未満であることとするNewton法で求めます.
典型的なパラメータでの推定結果 #
まずは,典型的なパラメータで推定できるかを確認します. 結果は以下のとおりで,正しく推定できていることがわかります.
| \(A\) | \(b\) | \(A\) の推定値 | \(b\) の推定値 |
|---|---|---|---|
| 1.0 | 1.0 | 0.999994 | 0.996397 |
| 5.0 | 2.0 | 4.999925 | 2.004784 |
| 1.0 | 0.1 | 0.984138 | 0.099924 |
乱数パラメータでの推定結果 #
次に, \(A\) , \(b\) をそれぞれ \(0.1\) 以上 \(5\) 以下の一様乱数で決めて,それらパラメータが推定できるかを確認します. パラメータ推定を1000回行い, \((A,b)\) によらず計算できるかを確認します.
実行した結果,計算が収束した割合は 98.3% でした. 1000回のうち17回は,Newton 法が収束せず,解が得られませんでした.
ここで,収束した場合としなかった場合でどのような差があるかを確認します.
まず,収束した場合の \(A\) , \(b\) の相対誤差は以下のとおりです2.
| 最小 | 中央 | 最大 | 平均 | 標本標準偏差 | |
|---|---|---|---|---|---|
| \(A\) | 3.41e-09 | 1.26e-05 | 6.75e-01 | 6.51e-03 | 5.02e-02 |
| \(b\) | 4.71e-06 | 7.18e-03 | 3.43e-01 | 1.63e-02 | 2.85e-02 |
次に,収束しない場合の,反復終了時点の \(A\) , \(b\) の相対誤差は以下のとおりです.
| 最小 | 中央 | 最大 | 平均 | 標本標準偏差 | |
|---|---|---|---|---|---|
| \(A\) | 2.68e-07 | 7.35e-06 | 3.81e-05 | 9.58e-06 | 9.36e-06 |
| \(b\) | 3.30e-02 | 1.15e-01 | 6.15e-01 | 1.66e-01 | 1.51e-01 |
\(b\) の相対誤差の平均値,中央値,最大値は,収束したかどうかで変わらないように見えます.一方で, \(b\) の相対誤差の最小値を比較すると,反復が終了した場合の方が誤差が小さいので,反復が収束する場合の方が精度よく求まるケースはあるようです. ですので,収束した場合に精度よく求まるケースが観測されたものの,収束したかどうかで精度が明確に異なるとも言い難いという結果になりました.
ところで,収束した場合の \(A\) の平均値が 2.59205, 収束しなかった場合の \(A\) の平均値が 0.234635 なので,切断点が小さいときに,収束が難しい可能性があります. \(A,b\) の組み合わせによる可能性もありますので,正確に条件を把握するために,計算に成功した場合と失敗した場合の \((A,b)\) をプロットしてみます.
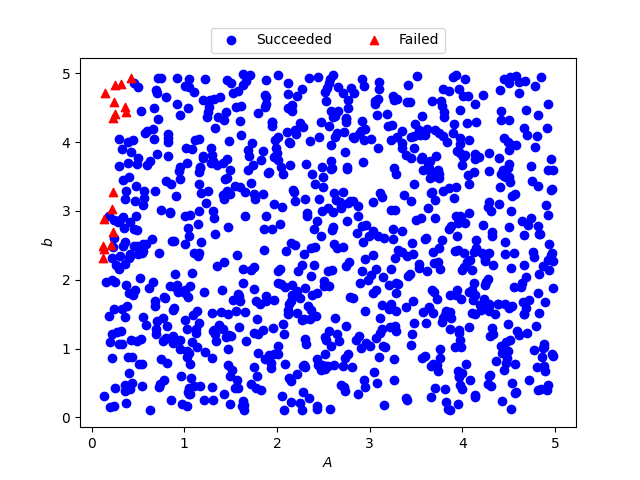
Figure 1. 計算に成功した場合と失敗した場合の \((A,b)\)
Fug. 1 より, \(A\) が小さく, \(b\) が大きい場合に失敗しやすいことがわかります.
まとめると,以下のようになります.
- 収束したかどうかで,精度が明確に異なるとは言い難い.
- 収束しても精度よく求まるとは限らないが,収束した場合に精度よく求まったケースはあった.
- \(A\) が小さく \(b\) が大きい場合に収束が難しい可能性がある.
以上より, \(b\) を数値的に求める方法に検討の余地があると考えられます.
Python による実装例 #
Python による実装例は以下のとおりです. また,本数値実験は,以下の実装で行いました.
import numpy as np
import scipy.stats as stats
def estimate(random_values):
a = np.max(np.abs(random_values))
m = np.mean(np.abs(random_values))
b = 1.0
max_loop = 100000
threshold = 1.0e-15
converged = False
for _ in range(max_loop):
exp_a_b = np.exp(a / b)
if np.abs(b - a / (exp_a_b - 1) - m) < threshold:
converged = True
break
c = a / (b * (exp_a_b - 1))
b -= (b - a/(exp_a_b - 1) - m)/(1 + c*c*exp_a_b)
if not converged:
raise RuntimeError('Did not converge. (A={}, b={})'.format(a, b))
exp_a_b = np.exp(a / b)
d = a / (exp_a_b - 1)
n = len(random_values)
f = -n*np.log(2*b*(1 - np.exp(-a / b))) - m*n / b
if f < -n*np.log(2*a):
raise RuntimeError('Failed.')
ddf = (n / b**4)*(d*d*exp_a_b - 2*b*d + b*(b - 2*m))
if ddf >= 0:
raise RuntimeError('Failed.')
return a, b
まとめ #
本ページでは,一部のパラメータが既知である,特殊なラプラス分布や切断ラプラス分布のパラメータ推定方法についてまとめました.
\(\mu=0\) のラプラス分布では, \(b\) が簡単に推定できますが,切断ラプラス分布の場合は,一般には数値的にしか求まらないことがわかりました.
数値実験では,典型的な例では,切断ラプラス分布のパラメータが推定できていそうな様子は確認できましたが,計算が収束しない場合があることもわかりました.
パラメータよらず,より確実にパラメータ推定を行う方法や,本ページの方法を,一般の切断ラプラス分布のパラメータ推定に拡張する方法は,現時点でわかっておらず,今後の課題です.
参考文献 #
[1] Wikipedia,“Laplace distribution - Wikipedia”, https://en.wikipedia.org/wiki/Laplace_distribution#Statistical_inference, 2024/6/6 最終アクセス.