サイコロをN回投げたときちょうど6回に1回の割合で1の目が出る確率 #
概要 #
前ページでは,サイコロを繰り返し投げる試行の確率モデルを定義しました.
本ページからは,サイコロを繰り返し投げると,およそ6回に1回程度の割合で1の目が出ることを確認します.
しかし,そもそもこれはどのように確認したらよいのでしょうか.
本ページではひとまず,ちょうど 6回に1回の割合で1の目が出る確率を計算してみます.
まず,サイコロを \(N\) 回投げたとき \(k\) 回だけ1の目が出る確率を求めます.その後,サイコロを繰り返し投げたとき,ちょうど 6回に1回の割合で1の目が出る確率を求めます.
サイコロをN回投げたときk回だけ1の目が出る確率 #
いま,確率空間 \((\Omega_N,\mathfrak{F}_N,P_N)\) を考えます. \(A_k=\{(\omega^j)\in\Omega_N\mid |\{j\mid \omega^j=\omega_1\}|=k\}\) とすると, \(A_k\) は \(N\) 回サイコロをなげて \(k\) 回だけ1の目が出た事象を表します.
\((\omega^j)\in A_k\) とすると, \(\omega^1,\omega^2,\dots,\omega^N\) のうち \(k\) 個が \(\omega_1\) ですが,これは \(N\) 個から \(k\) 個を選ぶ選び方を考えればよいので, \(\binom{N}{k}=N!/(k!(N-k)!)\) 個あります.
このとき,ある \(\{i_1,i_2,\dots,i_k\}\subset\{1,2,\dots,N\}\) について, \(k\) 個の要素 \(\omega^{i_j}\,(j=1,2,\dots,k)\) は \(\omega_1\) の1通りの値しかとれませんが,それ以外の \(N-k\) 個の要素は \(\omega_2,\omega_3,\dots,\omega_6\) の5通りの値をとれます.
したがって, \(|A_k|=\binom{N}{k}5^{N-k}\) とわかります.さらに, \(|\Omega_N|=6^N\) なので, \(P_N(A_k)=\binom{N}{k}5^{N-k}/6^N\) となります.
よって,以下のことがいえそうです.
Proposition 1. 偏りのないサイコロを \(N\) 回投げて \(k\) 回だけ1の目が出る確率は \[ \binom{N}{k}\frac{5^{N-k}}{6^N} \] となる.
ちょうど6回に1回の割合で1の目が出る確率 #
Prop. 1 を使って,ちょうど 6回に1回の割合で1の目が出る確率を計算してみます.
Prop. 1 より, \(N\) 回サイコロを投げて,ちょうど \(\lfloor N/6\rfloor\) 回1の目が出る確率 \(p(N)\) は,
\[ p(N)=\binom{N}{\lfloor N/6\rfloor}\frac{5^{N-\lfloor N/6\rfloor}}{6^N} \]と表せます.ただし, \(\lfloor x\rfloor=\max\{y\in\mathbb{Z}\mid y\le x\}\) とします.
\(N=1,2,\dots,1000\) の \(p(N)\) の値を図示すると以下のようになります.
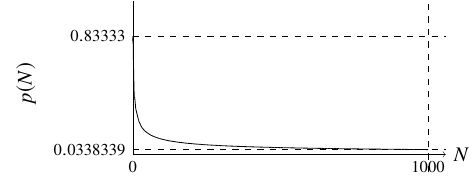
Figure 1. p(N) のグラフ
\(N\) を大きくすると,ちょうど 6回に1回の割合で1の目が出る確率は小さくなっていくことがわかります.たとえば, \(N=1000\) のときは \(3\%\) 程度なので,比較的まれな現象といえそうです.
つまり,サイコロを1回だけ投げて1の目が出る確率が \(1/6\) であるということは,ちょうど 6回に1回の割合で1の目が出るというわけではないことがわかりました.
まとめ #
本ページでは,サイコロを繰り返し投げるとき,ちょうど 6回に1回の割合で1の目が出る確率を計算しました.
その結果,確率としては小さい値となり,サイコロを1回だけ投げて1の目が出る確率が \(1/6\) であるということは,ちょうど 6回に1回の割合で1の目が出るというわけではないことがわかりました.