サイコロをN回投げたときおよそ6回に1回程度の割合で1の目が出ることの確率変数の導入による整理 #
概要 #
前ページまでで,サイコロを \(N\) 回投げるとき,次が成り立つことがわかりました.
- 確率が最大となる1の目の出る回数は \(N/6\) 程度である
- 平均的に \(N/6\) 回程度,1の目が出る
しかし,もとの“およそ6回に1回程度の割合で1の目が出る”という主張に対して,平均といった概念をもちだしているなど,直接的な結果に感じません.
そこで本ページでは,確率変数を導入することで,この問題をより取り扱いやすくして,およそ6回に1回程度の割合で1の目が出ることを,より直接的に示せないかを検討します.
確率変数 #
まずは,確率変数の定義について述べます.
Definition 1.
- \(A\) を集合,\(\mathfrak{F}\) をその完全加法族とする.一般に,\((A,\mathfrak{F})\) を 可測空間 という.また,\((A,\mathfrak{F}),(B,\mathfrak{G})\) を可測空間とするとき,関数 \(F:A\to B\) を \(F:(A,\mathfrak{F})\to(B,\mathfrak{B})\) と表す.
- \((A,\mathfrak{F}),(B,\mathfrak{G})\) を可測空間とする.関数 \(F:(A,\mathfrak{F})\to (B,\mathfrak{F})\) が,任意の \(b\in B\) について \(F^{-1}(b)=\{a\in A\mid F(a)=b\}\in\mathfrak{F}\) であるとき,関数 \(F\) を可測関数と呼ぶ.
- \(\mathbb{R}\) の開集合全体の集合を \(\mathfrak{O}(\mathbb{R})\) と表す.\(\mathfrak{O}(\mathbb{R})\) を含む最小の完全加法族を \(\mathfrak{B}(\mathbb{R})\) と表す.
- \(\Omega,\mathfrak{F}\) を標本空間とする,\(X:(\Omega,\mathfrak{F})\to(\mathbb{R},\mathfrak{B}(\mathbb{R}))\) が可測関数のとき,\(X\) を確率変数という.
なお,可測空間も標本空間も集合とその完全加法族の組なので,実質的には同じものですが,数理統計の文脈では,可測空間のことを標本空間と呼ぶ,という理解でよいです.また,本来は \(\mathfrak{B}(\mathbb{R})\) の存在を示す必要がありますが,ここでは認めるものとします.
\(X\) の像 \(X(\Omega)=\{x\in\mathbb{R}\mid \exists \omega\in\Omega\,(X(\omega)=x)\}\) が高々可算のとき, \(X\) は離散型確率変数と呼ばれます.
ここで,
\([X=x]=\{\omega\in\Omega_N\mid X(\omega)=x\}\)
とし,
\(P([X=x])\)
を \(P(X=x)\)
と略記することにします.
\([X
確率変数 \(X\) に対し, \(f_X:\mathbb{R}\to\mathbb{R}\) を \(f_X(x)=P(X\le x)\) と定め,確率関数, または確率質量関数と呼びます.
確率変数 \(X\) に対し, \(\mathbb{E}[X]=\sum_{x=0}^{\infty}xf_X(x)\) , \(\mathbb{V}[X]=\mathbb{E}[(X-\mathbb{E}[X])^2]\) を期待値, 分散といい,それぞれ平均と散らばりを表すと解釈されます.
このとき,以下の式が成り立つことが知られています.
Theorem 2 (Chebyshev の不等式). 任意の
\(\epsilon>0\) について,次の式が成り立つ. \[P(|X-\mathbb{E}[X]|\ge\epsilon)\le\frac{\mathbb{V}[X]}{\epsilon^2}\]
確率変数の導入 #
前ページの確率空間 \((\Omega_N,\mathfrak{F}_N,P_N)\) を考えます.本ページでは, \(N\) を省略し, \((\Omega,\mathfrak{F},P)\) と表すことにします.1の目が出た回数だけが問題のため,以下のような可測関数 \(X:(\Omega,\mathfrak{F})\to(\mathbb{R},\mathfrak{B}(\mathbb{R}))\) を考えます. \[ X(\omega^1,\omega^2,\dots,\omega^N)=|\{i\mid \omega^i=\omega_1\}|. \] このとき, \(x\notin\{0,1,\dots,N\}\) ならば \(X^{-1}(x)=\emptyset\in\mathfrak{F}\) であり, \(k\in\{0,1,\dots,N\}\) ならば \(X^{-1}(k)=\{(\omega^i)\in\Omega\mid |\{i\mid \omega^i=\omega_1\}|=k\}\in 2^{\Omega}=\mathfrak{F}\) なので \(X\) は確率変数です.
ここまで定めた記号で以下が成り立ちます.
Proposition 3. 以下が成り立つ.
\[ f_X(x)=\begin{cases} \displaystyle\binom{N}{x}\frac{5^{N-x}}{6^N},&x=0,1,\dots,N,\\ 0,&\mathrm{otherwise}. \end{cases} \]
二項分布の導入 #
一般に,確率変数 \(X\) の確率質量関数が \[ f_X(x)=\begin{cases} \displaystyle\binom{N}{x}p^x(1-p)^{N-x},&x=0,1,\dots,N,\\ 0,&\mathrm{otherwise} \end{cases} \] となるとき,確率変数 \(X\) は,パラメータ \((N,p)\) の二項分布に従うといいます.
二項分布の確率関数は,独立な試行を \(N\) 回繰り返したとき,確率 \(p\) で生起する事象が \(x\) 回発生する確率を表します.
二項分布については以下が成り立つことが知られています.
Theorem 4. 以下が成り立つ.
- \(\mathbb{E}[X]=Np\).
- \(\mathbb{V}[X]=Np^2\).
- \(f_X(x)\) が最大になる \(x\) は,\((N+1)p\) が整数のとき \((N+1)p-1,(N+1)p\), そうでないとき \(\lfloor(N+1)p\rfloor\) である.
確率関数が Prop. 2 となる確率変数は,パラメータ \(p\) が \(1/6\) である二項分布に従うといえます.
よって,Thm. 4.1 より, \(\mathbb{E}[X]=N/6\) , Thm.4.2 より \(f_X(x)\) が最大になる \(x\) はおよそ \(N/6\) 程度となりますが,これは前ページの結論に一致します.
サイコロをN回投げたときおよそ6回に1回程度の割合で1の目が出ることの新たな説明 #
さらに,Thm. 2 より,以下を示すことができます.ただし,パラメータ \((N,1/6)\) の二項分布に従う確率変数を \(X_N\) と表します.
Theorem 5. 任意の (\epsilon>0) について,以下が成り立つ.
\[\lim_{N\to\infty}P\left(\left|\frac{X_N}{N}-\frac{1}{6}\right|\ge\epsilon\right)=0\]
これは,例えば \(\epsilon=10^{-10}\) のような小さな値をとったとしても, \(N\) を十分大きくとると,サイコロを \(N\) 回投げて1の目が出た割合 \(X_N/N\) と \(1/6\) が \(\epsilon=10^{-10}\) 以上になる確率( \(1/6\) からほんの少しでもずれる確率)は0に近づく(ほとんど起こらなくなる)ということなので,サイコロを投げる回数 \(N\) を十分大きくとると,サイコロを \(N\) 回投げたときおよそ6回に1回程度の割合で1の目が出る ことを示しています.
大数の法則を用いた説明 #
Thm. 5 が,サイコロを \(N\) 回投げたときおよそ6回に1回程度の割合で1の目が出ることの,かなり直接的な説明を与えており,本節の目的は達成したといえます.
ただし,Thm. 5 は確率収束と呼ばれる収束性を用いて説明されますが,さらに強く,概収束と呼ばれる収束性を用いて説明できることが知られています.
Theorem 6. 以下が成り立つ.
\[P\left(\lim_{n\to\infty}\frac{X_N}{N}=\frac{1}{6}\right)=1\]
これは,サイコロを \(N\) 回投げて1の目が出た割合 \(X_N/N\) の \(N\) を大きくすると,ほとんど確実に \(1/6\) に収束することを表しています.これもかなり直接的に,サイコロを \(N\) 回投げたときおよそ6回に1回程度の割合で1の目が出る ことを示しています.
Thm. 5 の結果は大数の弱法則,Thm. 6 の結果は大数の強法則 と呼ばれる法則の特殊ケースです.どちらも,二項分布でなく,ベルヌーイ分布と呼ばれる分布を考えて,それぞれの法則をあてはめることで得られます.
コンピュータでのシミュレーション #
最後に,コンピュータによるシミュレーション結果について説明します.
大数の弱法則では, \(N\) を十分大きくすると, \(X_N/N\) が \(1/6\) から外れることはほとんどないことを主張しています.大数の強法則では, \(N\) を十分大きくすると, \(X_N/N\) はほとんど確実に \(1/6\) に近づくことを主張しています.
そこで,サイコロを1000回投げることをコンピュータ上でシミュレートし,サイコロを \(N\,(0\le N\le 1000)\) 回投げたとき1の目が出た回数の割合を求めてプロットします.これを数回繰り返し,各 \(N\) でどれくらいのばらつきがあるか, \(1/6\) に近づくかを確認します.
区間 \([0,1)\) 上の値を一様ランダムに返してくれる関数があるとします. ランダムに得られた \(y\in[0,1)\) に対し, \(x=\lfloor 6y\rfloor+1\) とすると,一様ランダムに \(\{1,2,\dots,6\}\) を返す関数をつくることができます.
これを利用して,サイコロを1000回投げることコンピュータでシミュレートし,それを4回繰り返した結果を図示したものは以下のとおりです.この4回の試行は4つの色で区別します.
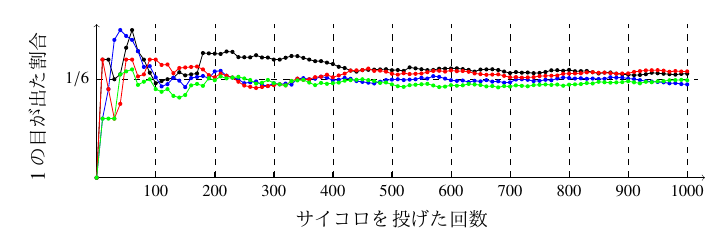
Figure 1. シミュレーション結果
Fig. 1 を見ると,100回までは結果にばらつきがありますが, \(N\) を大きくすると,ばらつきは小さくなり, \(1/6\) に近づいていることが確認できました.
まとめ #
本ページでは,確率変数を導入し,大数の弱法則,大数の強法則を用いることで,およそ6回に1回程度の割合で1の目が出ることを,より直接的に示せることを説明しました.
これは,公理的確率論が頻度主義的確率論と矛盾しないことの一例を確認したことになります.