サイコロをN回投げたときおよそ6回に1回程度の割合で1の目が出ることの確認 #
概要 #
サイコロを繰り返し投げると,およそ6回に1回程度の割合で1の目が出ることを確認したいと思いますが,ちょうど6回に1回の割合で出るわけではないことがわかりました.
そこで,本ページでは,およそ6回に1回程度の割合で出ることを確認する方法を考えます.
いま, \(p(N,k)=\binom{N}{k}5^{N-k}/6^N\) とします.
このとき,以下の方針が考えられます.
- \(p(N,k)\) が最大となる \(k\) が,およそ \(N/6\) であることを確認する.
- サイコロを繰り返し投げると,平均的に \(N/6\) 程度の回数だけ1の目が出ることを確認する.
1は, \(N\) を固定したとき,1の目が出る回数として最もあり得るのがおよそ \(N/6\) のときであることを確認する方針です.
2は,サイコロを \(N\) 投げる試行自体を繰り返すと,試行ごとにばらつきがあるが,平均的には \(N/6\) 回程度1の目が出ることを確認する方針です.
確率が最大となる1の目の出る回数がN/6程度であることの確認 #
まず, \(p(N,k)\) を数値的に計算してみます. \(N=10,100,1000\) の場合を計算しますが,値が小さくなりすぎるので, \(\log_{10}p(N,k)\) を計算することにします.
縦軸・横軸のスケールが各グラフで異なる点に注意してください.
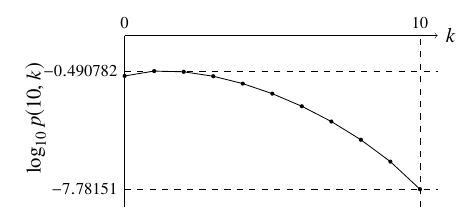
Figure 1. N=10の場合
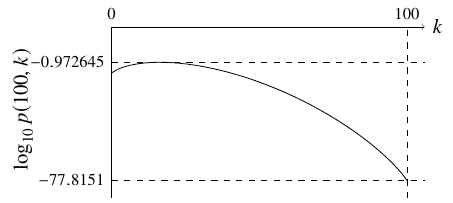
Figure 2. N=100の場合
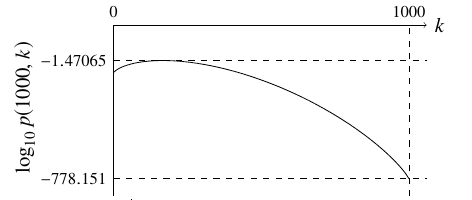
Figure 3. N=1000の場合
Figs. 1–3 より,
\(k=k_0\)
で \(p(N,k)\)
が最大になるとき,
\(k
\(p(N,k)>0\) なので, \(p(N,k+1)/p(N,k)\) を計算すると,
- \(p(N,k+1)/p(N,k)>1\) ならば \(p(N,k+1)>p(N,k)\) ,
- \(p(N,k+1)/p(N,k)=1\) ならば \(p(N,k+1)=p(N,k)\) ,
- \(p(N,k+1)/p(N,k)<1\)
ならば \(p(N,k+1)
となるので,隣り合う項の比を計算することで,頂点がわかるだろうと考えられます.
\[ \begin{aligned} &\frac{p(N,k+1)}{p(N,k)}\\ &=\frac{\binom{N}{k+1}5^{N-(k+1)}/6^N}{\binom{N}{k}5^{N-k}/6^N}\\ &=\frac{\binom{N}{k+1}}{\binom{N}{k}}\frac{5^{N-(k+1)}/6^N}{5^{N-k}/6^N}\\ &=\frac{N!/((k+1)!(N-k-1)!)}{N!/(k!(N-k)!)}\frac{5^{N-(k+1)}}{5^{N-k}}\\ &=\frac{k!}{(k+1)!}\frac{(N-k)!}{(N-k-1)!}\frac{5^{N-(k+1)}}{5^{N-k}}\\ &=\frac{1}{k+1}\cdot(N-k)\cdot\frac{1}{5}\\ &=\frac{1}{5}\left(-1+\frac{N+1}{k+1}\right) \end{aligned} \] が成り立ちます.よって, \[ \frac{p(N,k+1)}{p(N,k)}\begin{cases} >1&\mathrm{if}\ k<(N+1)/6-1,\\ =1&\mathrm{if}\ k=(N+1)/6-1,\\ <1&\mathrm{if}\ k>(N+1)/6-1 \end{cases} \] となります.つまり,およそ \((N+1)/6-1\approx N/6\) に確率のピークがあることがわかりました.
平均的にN/6回程度1の目が出ることの確認 #
\(A_k\) を前に定めたとおりとします.このとき, \(A_k\) は,サイコロを \(N\) 回投げて1の目が \(k\) 回出る事象を表し, \(\sum_{k=0}^NA_k=\Omega\) すなわち \(\sum_{k=0}^NP(A_k)=P(\sum_{k=0}^NA_k)=P(\Omega)=1 \) なので, \[ \mu_N=\sum_{k=0}^NkP(A_k)=\sum_{k=0}^Nk\binom{N}{k}\frac{5^{N-k}}{6^N} \] を計算することで,平均的に何回程度1の目が出るかを計算できそうです.
試しに, \(N=1,2,3\) のときを計算します.
\[ \begin{aligned} \mu_1&=\sum_{k=0}^1k\binom{1}{k}\frac{5^{1-k}}{6^1}=\frac{1}{6},\\ \mu_2&=\sum_{k=0}^2k\binom{2}{k}\frac{5^{2-k}}{6^2}\\ &=0+1\cdot2\cdot\frac{5}{6^2}+2\cdot1\cdot\frac{1}{6^2}\\ &=\frac{1}{3},\\ \mu_3&=\sum_{k=0}^3k\binom{3}{k}\frac{5^{3-k}}{6^3}\\ &=0+1\cdot3\cdot\frac{5^2}{6^3}+2\cdot3\cdot\frac{5}{6^3}+3\cdot1\cdot\frac{1}{6^3}\\ &=\frac{1}{2}. \end{aligned} \]\(N=1,2,3\) ではすべて \(\mu_N=N/6\) が成り立っています. したがって,すべての \(N\) で \(\mu_N=N/6\) が成り立つことを示せばよさそうです.
\(N=1\) のときは既に示した通り,成り立ちます.いま, \(N\ge1\) について, \(\mu_N=N/6\) であると仮定し, \(\mu_{N+1}=(N+1)/6\) であることを示します.
以下, \(\binom{N+1}{k}=\binom{N}{k}+\binom{N}{k-1}\) であることを使います.また, \(\binom{N}{N+1}=\binom{N}{-1}=0\) と解釈することとします.
まず, \[ \begin{aligned} \mu_{N+1}&=\sum_{k=0}^{N+1}k\binom{N+1}{k}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\sum_{k=0}^{N+1}k\left(\binom{N}{k}+\binom{N}{k-1}\right)\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\sum_{k=0}^{N+1}k\binom{N}{k}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &\qquad{}+\sum_{k=0}^{N+1}k\binom{N}{k-1}\frac{5^{(N+1)-k}}{6^{N+1}}\\ \end{aligned} \] となります.
第1項は, \[ \begin{aligned} &\sum_{k=0}^{N+1}k\binom{N}{k}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\frac{5}{6}\sum_{k=0}^Nk\binom{N}{k}\frac{5^{N-k}}{6^N}\\ &=\frac{5}{6}\cdot\frac{N}{6} \end{aligned} \] です.
第2項は, \[ \begin{aligned} &\sum_{k=0}^{N+1}k\binom{N}{k-1}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\sum_{k=1}^{N+1}k\binom{N}{k-1}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\sum_{k=0}^N(k+1)\binom{N}{k}\frac{5^{N-k}}{6^{N+1}}\\ &=\sum_{k=0}^Nk\binom{N}{k}\frac{5^{N-k}}{6^{N+1}}+\sum_{k=0}^N\binom{N}{k}\frac{5^{N-k}}{6^{N+1}}\\ \end{aligned} \] です.
この第1項は, \[ \begin{aligned} &\sum_{k=0}^Nk\binom{N}{k}\frac{5^{N-k}}{6^{N+1}}\\ &=\frac{1}{6}\sum_{k=0}^Nk\binom{N}{k}\frac{5^{N-k}}{6^N}\\ &=\frac{1}{6}\cdot\frac{N}{6} \end{aligned} \] で,第2項は, \[ \begin{aligned} &\sum_{k=0}^N\binom{N}{k}\frac{5^{N-k}}{6^{N+1}}\\ &=\frac{5^N}{6^{N+1}}\sum_{k=0}^N\binom{N}{k}5^{-k}\\ &=\frac{5^N}{6^{N+1}}\sum_{k=0}^N\binom{N}{k}\left(\frac{1}{5}\right)^k1^{N-k}\\ &=\frac{5^N}{6^{N+1}}\left(\frac{1}{5}+1\right)^N\\ &=\frac{5^N}{6^{N+1}}\left(\frac{6}{5}\right)^N\\ &=\frac{1}{6} \end{aligned} \] なので,あわせて \(N/6^2+1/6\) となります.
したがって, \[ \begin{aligned} \mu_{N+1}&=\sum_{k=0}^{N+1}k\binom{N+1}{k}\frac{5^{(N+1)-k}}{6^{N+1}}\\ &=\frac{5N}{6^2}+\left(\frac{N}{6^2}+\frac{1}{6}\right)\\ &=\frac{N}{6}+\frac{1}{6}\\ &=\frac{N+1}{6} \end{aligned} \] が成り立ちます.
以上より,数学的帰納法によって,すべての \(N\) で \(\mu_N=N/6\) が成り立ちます.
したがって,偏りのないサイコロを \(N\) 回投げたとき,平均的に \(N/6\) 回,1の目が出ることがわかりました.
まとめ #
本ページでは,サイコロを繰り返し投げると,およそ6回に1回程度の割合で1の目が出ることを確認しました.具体的には,サイコロを \(N\) 回投げるとき,次が成り立つことがわかりました.
- 確率が最大となる1の目の出る回数は \(N/6\) 程度である
- 平均的に \(N/6\) 回程度,1の目が出る