多様体上の数理最適化 #
概要 #
特定の制約のもとで与えられた関数を最小化または最大化する問題を 最適化問題 と呼び,何らかの条件のもとでよいものを選択する実世界の問題を,最適化問題に定式化してその解を求めることを 数理最適化 といいます.
近年,多様体 と呼ばれる空間の上での関数に対する最適化問題を考えることが,応用上有用であるとして注目されているようです.
本ページでは,[1] を一読した記録として,多様体上の数理最適化の実行例について述べます.
実験用に使ったプログラムは以下に配置しています.
文献 [1] 初読時の記録 #
文献 [1] 初読時の感想やメモは,X 上の次のリプライツリーで投稿しています.
多分に誤りを含むものと思いますが,記録のためにリンクを貼っておきます.
[佐藤 寛之,多様体上の最適化理論,オーム社,2024] を購入.確かに丁寧ではあるけれど,本題の第III部にたどり着けるかしら.まえがきに,不要ならこんな感じにスキップしながら読んでいいよとあるので,そうしようかな.https://t.co/bommzuzK2f
— htakeuchi0 (@htakeuchi0) January 30, 2024
はじめに:多様体と最適化問題 #
通常の微積分は, \(\mathbb{R}^n\) という,実数またはその組全体がつくる空間で議論されます. ここではその空間のことを ユークリッド空間 と呼んでおきます.
そうではない一般の空間においても,実数の組で表される座標というものをいい感じに導入して,もとの空間の代わりにその座標で考えることにすれば,通常の微積分が一般の空間でも使えそうです.
また, \(\mathbb{R}^n\) の部分空間であっても,通常とは別の座標を導入してそこで議論したい場合にも,この考え方が使えそうです.
もっとも,“いい感じ” に導入できていないと議論に不都合がでてくるので,なんでもよいわけではありません.
多様体 とは,上記の要領で \(\mathbb{R}^n\) の議論を抽象化して規定された “いい感じ” の空間であり,リーマン多様体 とは,特にそこにより扱いやすくするための条件を加えたものになります.
ところで,最適化問題には以下の分類があります.
- 無制約最適化問題
- 制約付き最適化問題
制約付き最適化問題というのは,“ある条件を満たすものの中で最適なものを求めよ” という問題です. 例えば,球面上の関数を最小にする点を求めよ,という問題は,制約付き最適化問題となります.
球面に “いい感じ” に座標を設定すればリーマン多様体とみなせることが知られています. 地球は3次元空間に浮いていますが,2次元平面の地図や,それを集めた地図帳が作れる,ということがそれを示唆しています. すると,球面上の最適化問題は,もともと制約付き最適化問題であったものを,リーマン多様体上の無制約最適化問題とみることができます.
一般に,制約付き最適化問題は無制約最適化問題より難しい問題なので,制約付き最適化問題を多様体上の無制約最適化問題とみることで,通常の方法とは異なる解き方を考える余地が生まれます.
本ページでは,球面よりさらに簡単に,円周上の最適化問題を例示します. 小さすぎる例ではありますが,導入としてはこれくらい単純な方がよいと考えるためです.
本ページで対象とする最適化問題 #
本ページでは,以下の形の問題を解くことを考えます.
\[ \begin{aligned} &\mathrm{Minimize}\ x^TAx\\ &\mathrm{subject\ to}\ x^Tx=1. \end{aligned} \]ただし, \(A\in\mathbb{R}^{n\times n},x\in\mathbb{R}^n\) であり, \(A\) は与えられるものとします. また, \(\mathbb{R}^{n\times n}\) で, \(n\times n\) 型行列全体の集合を表すことにします.
本ページでは特に, \(n=2\) を考え,具体的には以下の問題を解くことにします. \(x\in\mathbb{R}^2\) です.
\[ \begin{aligned} &\mathrm{Minimize}\ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x\\ &\mathrm{subject\ to}\ x^Tx=1. \end{aligned} \]この制約条件は \(S^{n-1}=\{x\in\mathbb{R}^n\mid x^Tx=1\}\) によって, \(x\in S^1\) と表すことができます. \(S^{n-1}\) は \((n-1)\) 次元球面と呼ばれる多様体です. \(n=2\) のとき,つまり \(S^1\) は 半径1の円周 を表します.
以上より,本ページで対象とする最適化問題を,以下のように表現しておきます.
\[ \begin{aligned} &\mathrm{Minimize}\ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x\\ &\mathrm{subject\ to}\ x\in S^1. \end{aligned} \]厳密解 #
数値的に解を求める前に,この問題の厳密解を解析的な方法で求めます.
この最適化問題は, ラグランジュの未定乗数法 という方法で解くことができます. この解析的な方法はユークリッド空間上で考えればよく,多様体を意識する必要はありません.
この問題の場合,ラグランジュの未定乗数法によると, \(x^*\) が局所的最適解であるとき, \(\lambda^*\in\mathbb{R}\) が存在し, \[ \begin{aligned} &\left.\frac{\partial}{\partial x_1}\left(x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x+\lambda(x^Tx-1)\right)\right|_{x=x^*, \lambda=\lambda^*}=0,\\ &\left.\frac{\partial}{\partial x_2}\left(x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x+\lambda(x^Tx-1)\right)\right|_{x=x^*, \lambda=\lambda^*}=0,\\ &\left.\frac{\partial}{\partial \lambda}\left(x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x+\lambda(x^Tx-1)\right)\right|_{x=x^*, \lambda=\lambda^*}=0 \end{aligned} \] を満たします. ただし, \(x\) の第 \(i\) 要素を \(x_i\) と表します.
よって,以下の方程式を解くと,解の候補が得られることになります. \[ \begin{aligned} &10x_1+4x_2+2\lambda x_1=0,\\ &4x_1+6x_2+2\lambda x_2=0,\\ &x_1^2+x_2^2-1=0. \end{aligned} \] 上2つの式は, \[ \begin{aligned} &(10+2\lambda)x_1+4x_2=0,\\ &4x_1+(6+2\lambda)x_2=0 \end{aligned} \] と書けて,それぞれの両辺を2で割って,第2式の \((-1/2)(5+\lambda)\) を第1式にたすと, \[ \begin{aligned} &\left(2-\frac{1}{2}(3+\lambda)(5+\lambda)\right)x_2=0,\\ &2x_1+(3+\lambda)x_2=0 \end{aligned} \] となります.
これが解をもつには, \[ \begin{aligned} &2-\frac{1}{2}(3+\lambda)(5+\lambda)=0,\\ &2x_1+(3+\lambda)x_2=0 \end{aligned} \] が必要なので,復号同順で \[ \begin{aligned} &\lambda=-4\pm\sqrt{5},\\ &x_2=-\frac{1\pm\sqrt{5}}{2}x_1 \end{aligned} \] が得られます.
次に, \(x_1^2+x_2^2=1\) なので, \[ 1=x_1^2+x_2^2=x_1^2+\left(-\frac{1\pm\sqrt{5}}{2}x_1\right)^2 \] から, \[ x_1=\sqrt{\frac{5\pm\sqrt{5}}{10}},-\sqrt{\frac{5\pm\sqrt{5}}{10}} \] が得られ, \((x_1,x_2)\) としては, \[ \begin{aligned} &\left(\sqrt{\frac{5-\sqrt{5}}{10}},-\frac{1+\sqrt{5}}{2}\sqrt{\frac{5-\sqrt{5}}{10}}\right),\\ &\left(-\sqrt{\frac{5-\sqrt{5}}{10}},\frac{1+\sqrt{5}}{2}\sqrt{\frac{5-\sqrt{5}}{10}}\right),\\ &\left(\sqrt{\frac{5+\sqrt{5}}{10}},-\frac{1-\sqrt{5}}{2}\sqrt{\frac{5+\sqrt{5}}{10}}\right),\\ &\left(-\sqrt{\frac{5+\sqrt{5}}{10}},\frac{1-\sqrt{5}}{2}\sqrt{\frac{5+\sqrt{5}}{10}}\right) \end{aligned} \] が得られます. また,複号同順で \[ (x_1,x_2)=\left(\pm\sqrt{\frac{5-\sqrt{5}}{10}},\mp\frac{1+\sqrt{5}}{2}\sqrt{\frac{5-\sqrt{5}}{10}}\right) \] のとき, \[ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x=4-\sqrt{5} \] で,複号同順で \[ (x_1,x_2)=\left(\pm\sqrt{\frac{5+\sqrt{5}}{10}},\mp\frac{1-\sqrt{5}}{2}\sqrt{\frac{5+\sqrt{5}}{10}}\right) \] のとき, \[ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x=4+\sqrt{5} \] です.
以上より,最小解は \[ (x_1,x_2)=\left(\pm\sqrt{\frac{5-\sqrt{5}}{10}},\mp\frac{1+\sqrt{5}}{2}\sqrt{\frac{5-\sqrt{5}}{10}}\right) \] であって,そのときの目的関数の値は \[ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x=4-\sqrt{5} \] となります.
目的関数の等高線は以下 (Fig. 1) の通りで,▲は上記で計算した最小解です.
参考のため,最大解を●で表します.
中央の太い円が制約式の示す円周です.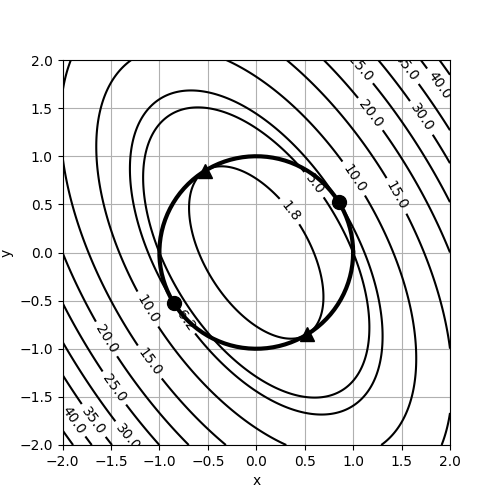
Figure 1. 目的関数の等高線.太い円が等式制約,▲が最小解,●が最大解.
Fig. 1より,▲における関数値より値が小さくなる点が存在しないことがわかるので,正しく計算できていることがわかります. また,最小解も最大解も,制約式のグラフと等高線のグラフの接点であることもわかります. 実は,ラグランジュの未定乗数法は,そのような点を計算していたのでした.
数値解法 #
本節では,前節で得られた厳密解を,数値的に求めることを考えます.
いま, \(S^1\) はリーマン多様体なので,本ページで解こうとしている問題は,実行可能集合が多様体全体となり,多様体上の無制約最適化問題とみなせます.
通常のユークリッド空間では,無制約最適化問題の解法は,直線探索に基づく手法が典型的です. これは,その時点で得られている近似解に対して,目的関数値が減少する方向に少しずつ解を更新し,最適解を求める方法です.
ユークリッド空間の場合,無制約最適化問題の数値解法では,得られている近似解 \(x_k\in\mathbb{R}^n\) に対し,探索方向 \(d_k\in\mathbb{R}^n\) とステップ幅 \(t_k>0\) を計算し, \(x_{k+1}=x_k+t_kd_k\) によって解を更新します. この \(d_k\) や \(t_k\) は,目的関数の値が下がると期待される方向や量で決めます. 例えば,目的関数が \(f:\mathbb{R}^n\to\mathbb{R}\) のとき, \(d_k=-\nabla f(x_k)\) , \(t_k\) は (strong) Wolfe 条件 と呼ばれる条件を満たすようにとる方法があります.ここで, \(\nabla\) は勾配を表します.
リーマン多様体の場合も同様の考え方で近似解を更新して求めます. リーマン多様体では,勾配 \(\nabla\) の代わりに,リーマン計量から定まる勾配(リーマン勾配) \(\mathrm{grad}\) によって, \(-\mathrm{grad}\ f(x_k)\) を考えることができるので, \(d_k=-\mathrm{grad}\ f(x_k)\) と計算できます. また,ステップ幅 \(t_k>0\) に対して, \(t_kd_k\) を考えることもできます. しかし,一般のリーマン多様体では, \(x_k\) と \(d_k\) は異なる空間のものなので, \(x_k+t_kd_k\) というものを考えることができません. したがって,これに相当する概念が必要となります. この概念があれば,(strong) Wolfe 条件もリーマン多様体上の条件に拡張できます.
リーマン多様体を \(\mathcal{M}\) と表すと,ユークリッド空間の勾配に相当する リーマン勾配 は接束 \(T\mathcal{M}\) と呼ばれる空間に属します. \(x_k\in\mathcal{M}\) と \(t_kd_k\in T\mathcal{M}\) の和が定義できないので,勾配 \(d_k\in T\mathcal{M}\) を多様体 \(\mathcal{M}\) 上の曲線に対応させ, \(x_k+t_kd_k\) の代わりに, 多様体上の点 \(x_k\) を通る多様体 \(\mathcal{M}\) 上の曲線に沿って \(d_k\) 方向に \(t_k\) の幅だけ進む,ということを考えます. これには, \(R:T\mathcal{M}\to\mathcal{M}\) という,接ベクトルと多様体上の点を対応させる写像があればよく, \(x_{k+1}=x_k+t_kd_k\) の代わりに \(x_{k+1}=R_{x_k}(t_kd_k)\) の形で近似解を更新することを考えます. この写像 \(R\) を レトラクション といいます.
さて,本ページの問題の場合の具体的な計算方法について考えます. まず, \(x_k\in S^1\) に対する \(d_k=-\mathrm{grad}\ f(x_k)\) は, \(\mathrm{grad}\ f(x)=(I-xx^T)\nabla f(x)\) によって具体的に計算できます. ここで, \(I\) は恒等行列です.
例として,目的関数 \(f\) を \[ f(x)=x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x \] とした場合の, \(x_0=(1/\sqrt{2},1/\sqrt{2})\in S^1\) に対する \(\nabla f(x_0)\) と \(\mathrm{grad}\ f(x_0)\) は以下のようになります.
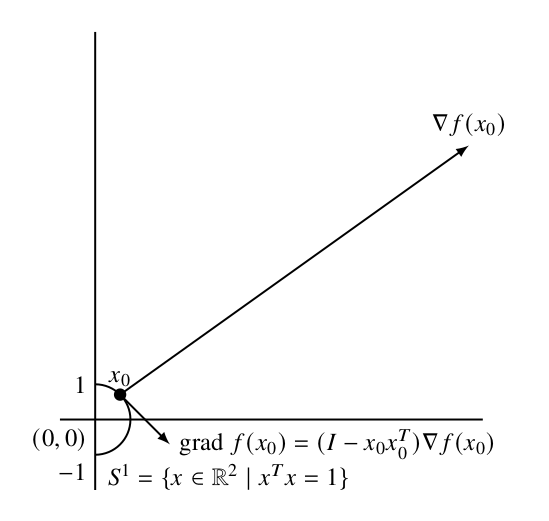
Figure 2. \(\nabla f(x_0)\) と \(\mathrm{grad}\ f(x_0)\)
\(d_k=-\mathrm{grad}\ f(x_k)\) とすると \(d_k\sub\mathbb{R}^2\) にはなりますが, \(x_k+t_kd_k\in\mathbb{R}^2\) は一般に \(S^1\) に属しませんので,やはり単純には解の更新はできません.そこでレトラクションにより \(x_{k+1}=R_{x_k}(t_kd_k)\) と更新することを考えます.
本ページでは,レトラクション \(R\) を \[ R_x(d)=\frac{x+d}{\|x+d\|_2} \] と定義します. 多様体 \(S^1\) の点 \(x\) における接ベクトル \(d\in TS^1\) を \(R_x(d)\in S^1\) によって多様体上の点に対応付けています. \(\phi(t)=R_x(td)\,(t\ge0)\) とすると,接ベクトル \(d\) の方向が決める多様体上の曲線ができます.
この \(R\) がレトラクションの定義を満たすことは確認できますが,ここでは \(T\mathcal{M}\) も \(R\) も定義していないので,詳しく述べません. また,このレトラクションは,単に 正規化しているだけのもの といえますが,これ以外のレトラクションも考えられます.
先ほどの例において, \(t_0=0.2\) とした場合の \(x_0+t_0d_0\) と \(R_{x_0}(t_0d_0)\) は以下のようになります. \(x_0+t_0d_0\) は \(S^1\) の外に出てしまうので,レトラクションを利用して,正規化することで,更新後の近似解 \(x_1\in S^1\) を求めていることがわかります.
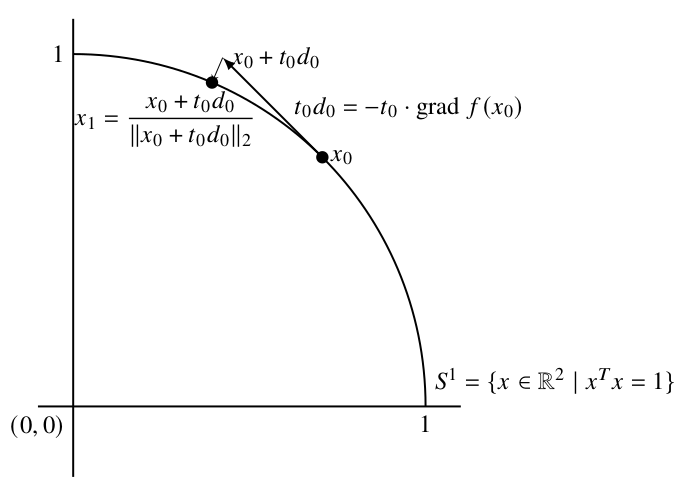
Figure 3. レトラクションの例
とにかくこれで,本ページの問題 \[ \begin{aligned} &\mathrm{Minimize}\ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x\\ &\mathrm{subject\ to}\ x\in S^1 \end{aligned} \] を,リーマン多様体の無制約最適化問題とみて数値計算ができるようになりました.
手順としてまとめると以下のようになります.
- Input: \(x_0\in S^1\)
- Output: 最適化問題の近似解
- for \(k=0,1,2,\dots\) do
- \(\quad d_k\leftarrow-2(I-x_kx_k^T)\begin{pmatrix}5&2\\2&3\end{pmatrix}x_k\)
- \(\quad t_k>0\) を決める.
- \(\quad x_{k+1}\leftarrow(x_k+t_kd_k)/\|x_k+t_kd_k\|_2\)
- \(\quad\) 収束判定条件を満たすなら \(x_{k+1}\) を返して終了.
- end for
数値例 #
本節では,以下の問題を数値的に解いた場合の例を示します.
\[ \begin{aligned} &\mathrm{Minimize}\ x^T\begin{pmatrix}5&2\\2&3\end{pmatrix}x\\ &\mathrm{subject\ to}\ x\in S^1. \end{aligned} \]ステップ幅は,本来は (strong) Wolfe 条件を満たすようにとるべきですが,ここでは簡単のため \(t_k=0.2\) とします.
初期値は \(x_0=(1/\sqrt{2},1/\sqrt{2})\in S^1\) とし,近似解の更新のようすをとらえることを目的として,収束判定は省略し,反復回数を128回とします.
以上より,本節の解法の具体的な手順は以下のようになります.
- Input: \(x_0=(1/\sqrt{2},1/\sqrt{2})\in S^1\)
- Output: 最適化問題の近似解 \(x_{128}\)
- for \(k=0,1,2,\dots,127\) do
- \(\quad d_k\leftarrow-2(I-x_kx_k^T)\begin{pmatrix}5&2\\2&3\end{pmatrix}x_k\)
- \(\quad t_k\leftarrow 0.2\)
- \(\quad x_{k+1}\leftarrow(x_k+t_kd_k)/\|x_k+t_kd_k\|_2\)
- end for
この手順をC++で実装・実行し,解の更新の様子を図示すると以下のようになります. リーマン勾配にそって近似解を仮に更新し,飛び出してしまったものをレトラクションにより \(S^1\) に落とすことを繰り返し,真の解に近づいていることがわかります.
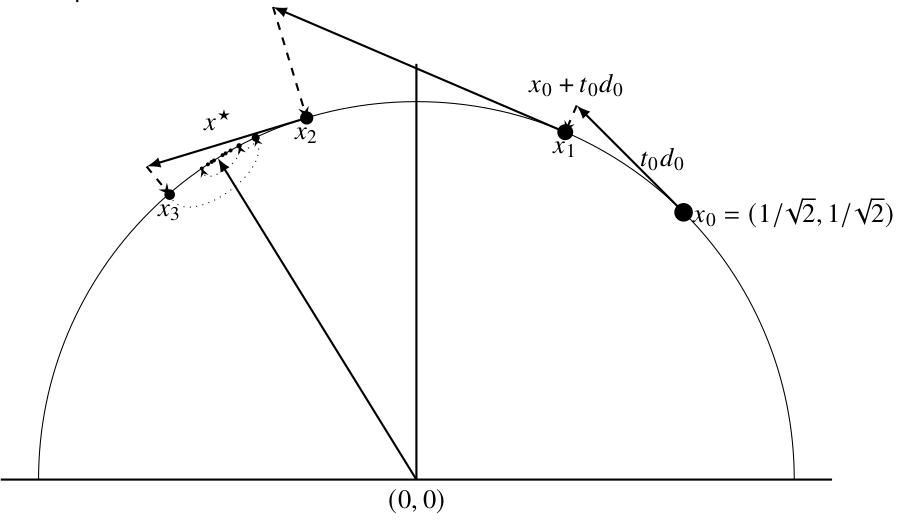
Figure 4. 実行例
すでに計算した結果から,このときの収束先 \(x^*\) は \[ x^*=\left(-\sqrt{\frac{5-\sqrt{5}}{10}},\frac{1+\sqrt{5}}{2}\sqrt{\frac{5-\sqrt{5}}{10}}\right) \] と考えられます.
この値を真の解として,各反復における近似解と真の解の相対誤差を計算すると以下のようになり,1次収束していることがわかります.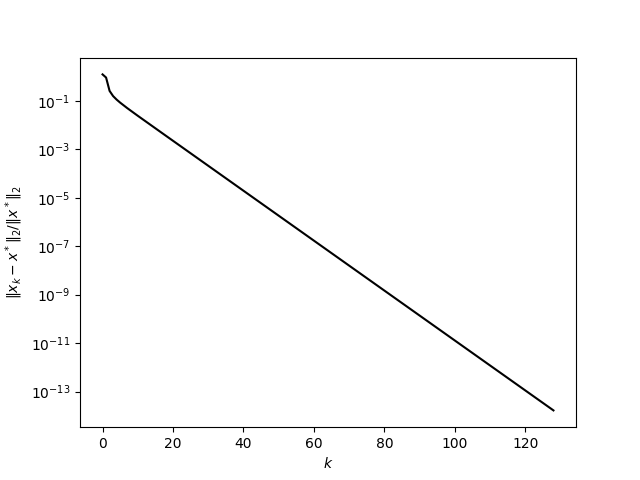
Figure 5. 相対誤差の履歴
実験用に使ったプログラムは以下に配置しています.
汎用性は低く,本ページの設定で実行できる程度の簡単なものです.
まとめ #
本ページでは,[1] を一読した記録として,多様体上の数理最適化の実行例について述べました.
簡単な \(S^1\) 上の最適化問題の数値例を示しました. C++でアルゴリズムを実装・実行したところ,近似解が真の解に近づき,1次収束している様子が観察できました.