行列を表現するデータ構造と行列積の計算時間 #
概要 #
\(A=(a_{ij})\) , \(B=(b_{ij})\) を \(n\) 次正方行列とします. 行列 \(A\) , \(B\) の積 \(AB\) は \[ (AB)_{ij}=\sum_{k=0}^{n-1}a_{ik}b_{kj},\quad 0\le i < n,\quad 0\le j < n \] と定義されます1.ただし,行列 \(M\) に対して, \((M)_{ij}\) で \(M\) の第 \((i,j)\) 成分を表します.
本ページでは,この行列積を,C++を用いていくつかの方針で実装し,実装方針による実行時間を比較します.
実験用に使ったプログラムは以下に配置しています.
以下, \(n=256\) とし, \(A\) , \(B\) の要素は倍精度浮動小数点数とします.
行列を表現するデータ構造と手順 #
はじめに,最も素朴な方法として,
\(A\)
, \(B\)
を2次元配列で表現することを考えます.
\(n\)
を定数 kN で表すとき,変数の宣言方法として,以下が考えられます.
double a[kN][kN];std::array<std::array<double, kN>, kN> a;double **a = new double*[kN]; ...std::vector<std::vector<double>> a;
これらはいずれも,a[i][j] が \(a_{ij}\)
を表すため,直感的です.
これらにそれぞれ,
mdim_raw_arraymdim_std_arraymdim_new_arraymdim_vector
というラベルをつけておきます.
また行列は,1次元配列で表現することもできます. C++では列指向と呼ばれる格納方法が一般的と思います. この場合,変数の宣言方法として,以下が考えられます.
double a[kN * kN];std::array<double, kN * kN> a;double *a = new double[kN * kN];std::vector<double> a;
これらはいずれも a[i + kN*j] が \(a_{ij}\)
を表します.
このデータ構造は,a[0], a[1], … の順に要素を参照すると,
\(a_{00}, a_{10}, ...\)
と,列方向に要素を順に参照することと,すべての要素が連続したメモリ空間に配置されることです2.
これらにそれぞれ,
sdim_raw_arraysdim_std_arraysdim_new_arraysdim_vector
というラベルをつけておきます.
さて,C++では,配列の飛び飛びの要素にアクセスするより,ひとつずつ参照先を進めていくようなアクセスの方が高速です.
ここで,行列積の定義は, \[ (AB)_{ij}=\sum_{k=0}^{n-1}a_{ik}b_{kj},\quad0\le i < n,\quad0\le j < n \] であり, \(b_{kj}\) は,“ひとつずつ参照先を進めていくようなアクセス” となりますが, \(a_{ik}\) はそうなりません.
そこで, \(\cdot^T\) を転置作用素としたとき, \(C=AB=(A^T)^TB\) と解釈し,
- \(A'\leftarrow A^T\)
- \(C\leftarrow A'^TB\)
とすると, \(a_{ik}=(A)_{ik}=(A')_{ki}\) なので, \[ (AB)_{ij}=\sum_{k=0}^{n-1}a_{ik}b_{kj}=\sum_{k=0}^{n-1}(A')_{ki}b_{kj},\quad0\le i < n,\quad0\le j < n \] と書けるため,行列積の演算を “ひとつずつ参照先を進めていくようなアクセス” のみで実現できます. これは,ライブラリの機能でいえば, \((A,B)\mapsto AB\) という関数の代わりに, \((A,B)\mapsto A^TB\) という関数を公開することと同じです.
sdim_{raw_array, std_array, new_array, vector} に対して,上記のように実装するものを,
sdim_raw_array_transsdim_std_array_transsdim_new_array_transsdim_vector_trans
とラベルづけしておきます. なお,本ページでは, \(A'\leftarrow A^T\) の部分は,in-place でなく,copy で実現します.つまり, \(A\) から新しい行列 \(A'\) を一から作成します. これは,非破壊的な実装で統一するためです. \(A\) が対称行列の場合,不要な処理が含まれているともいえます.
以上の12種類の実装方法を比較します.
数値実験 #
前節で述べた12種類の方法で行列積を実装し,実行時間を比較します.
コンパイラは g++ を使い,最適化レベル -O0, -O1, -O2, -O3 で実行します.
実行時間は,以下の手順で計測します.
- 行列積の演算を続けて10回行い,その開始時刻と終了時刻の差を10で割る.
- その操作を100回行い,その平均値を計測結果として採用する.
計測対象を10回分とするのは,1回あたりの行列積演算が短い時間で終わり,正確に実行時間が測定できないことに対する対策です. 100回繰り返すのは,標本標準偏差の形で環境誤差を測定できるようにするためです. なお,計測対象は,行列積演算部分のみ(転置をとるものはその処理を含む)で,積をとる行列を用意するための処理は含みません.
実行環境は以下のとおりです.
- CPU: 13th Gen Intel(R) Core(TM) i7-1360P (16コア)
- メモリ: 16.0GiB
- OS: Linux (Ubuntu 22.04.3 LTS)
- コンパイラ: g++ (Ubuntu 11.4.0-1ubuntu1~22.04) 11.4.0
実行結果は以下のとおりです. ばらつきが小さく,ほとんど見えませんが,エラーバーは標本標準偏差です.
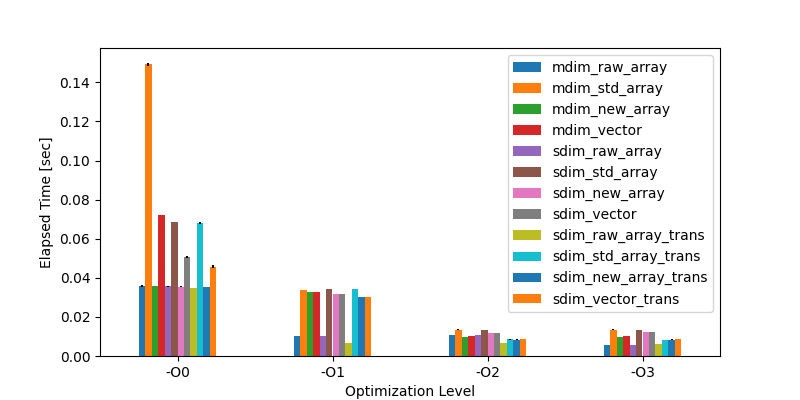
Figure 1. 実行結果
| Elapsed Time [sec] | -O0 | -O1 | -O2 | -O3 |
|---|---|---|---|---|
| mdim_raw_array | 0.035729 | 0.010241 | 0.010599 | 0.005580 |
| mdim_std_array | 0.149306 | 0.033978 | 0.013543 | 0.013524 |
| mdim_new_array | 0.035588 | 0.032892 | 0.009592 | 0.009589 |
| mdim_vector | 0.072027 | 0.032915 | 0.010311 | 0.010323 |
| sdim_raw_array | 0.035579 | 0.010249 | 0.010552 | 0.005586 |
| sdim_std_array | 0.068628 | 0.034363 | 0.013282 | 0.013329 |
| sdim_new_array | 0.035489 | 0.031903 | 0.011980 | 0.012386 |
| sdim_vector | 0.050499 | 0.031817 | 0.011980 | 0.012387 |
| sdim_raw_array_trans | 0.034581 | 0.006744 | 0.006732 | 0.006378 |
| sdim_std_array_trans | 0.068082 | 0.034350 | 0.008528 | 0.008408 |
| sdim_new_array_trans | 0.035308 | 0.030316 | 0.008321 | 0.008425 |
| sdim_vector_trans | 0.045771 | 0.030420 | 0.008486 | 0.008491 |
最も実行時間が短かったのは,-O3 の最適化レベルで,2次元の生配列で表した場合で,0.005580秒でした.
逆に,最も実行時間がかかったのは,-O0 の最適化レベルで,2次元の std::array で表した場合で,0.149306秒でした.
その比は26.76なので,最適化レベルや実装方針による性能の違いが大きいことがわかります.
なお,最適化なし (-O0) では手法ごとの差が顕著にあり,最適化レベル1 (-O1) でもまだ見られますが,最適化レベル2, 3 (-O2, -O3) では小さくなっていることがわかります.
そこで,以下の方針ごとに,実装手法の平均値を求めて図示すると以下のようになります.
- 2次元配列で表現する場合 (
mdim) - 1次元配列で表現する場合 (
sdim) - 1次元配列で表現して転置を取る場合 (
sdim_trans)
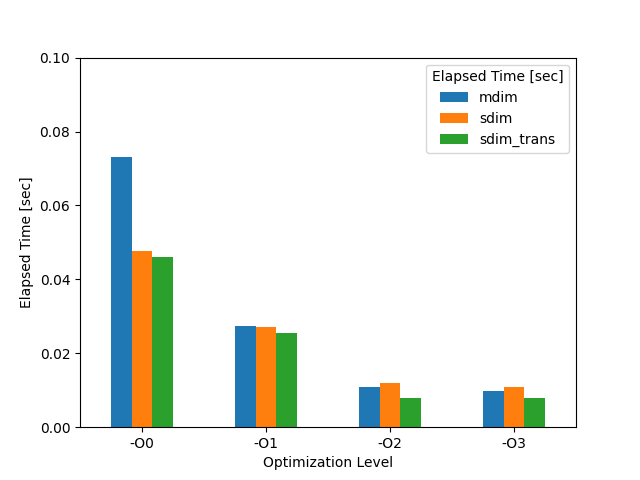
Figure 2. 方針ごと実行結果
最適化レベル2, 3 では,2次元配列で表現する場合 (mdim),1次元配列で表現する場合 (sdim),1次元配列で表現して転置を取る場合 (sdim_trans),の各方針を比較すると,1次元配列で表現して転置をとる場合 (sdim_trans) の実行時間が短いことがわかります.
転置をとる場合は,転置行列のコピーまで実行時間に含めているため,それを行ってもなお高速であるということもわかります.
まとめ #
本ページでは,行列積を,C++を用いていくつかの方針で実装し,実装方針による実行時間を比較しました.
実験の結果,最適化レベルや実装方針による性能の違いが大きいことがわかり,-O3 の最適化レベルで,2次元の生配列で表した場合が最も高速に計算できることがわかりました.
一方で,配列として表現するには,コンパイル時に行列サイズがわかっている必要があります.
それが困難な場合は,ヒープ領域上に動的に確保する必要がありますが,特に1次元配列の場合は,new で確保する場合と std::vector で確保する場合にあまり差がないので,行列は std::vector の1次元配列で表現して転置をとる,という方法が有用そうといえます.
したがって,本ページで実験した範囲に限り,実験結果から得られる結論としては,行列積演算の実行時間だけに着目すると,最適化レベルは3 (-O3) として,以下のようにすることがよいとわかります.
- コンパイル時に行列サイズがわかっている場合:行列を2次元の生配列で表現する
- コンパイル時に行列サイズがわかっていない場合:
std::vectorの1次元配列で表現して転置をとる