行列積の計算時間のCPU拡張命令による高速化 #
概要 #
前ページ では,OpenMP を用いることで,行列積演算の実行時間が短縮できることを確認しました.
これは,直列に実行する処理を,並列に行うことで実行時間の短縮を図ったものですが,同様の効果を狙う別の方法として,SIMD (Single Instruction, Multiple Data) と呼ばれる方法があります. これは,一つの命令を複数のデータに同時に適用することをいいます.
この方法は,CPUの拡張命令を用いて実現できます. Intel CPU では,Intel Intrinsics API という,CPUの命令セット拡張へのアクセスができるAPIを公開しています [1].
C++17 では,例えばヘッダファイル <immintrin.h> をインクルードすることで,AVX2 という拡張機能が使え,コンパイル時に -march=native -mavx2 というフラグを追加すると,AVX2 による命令を実行するプログラムが作成できます.
本ページでは,Intel CPU の拡張命令を用いて,SIMD により行列積演算の実行時間が短縮できることを確認します.
実験用に使ったプログラムは以下に配置しています.
CPU拡張命令の利用 #
まず,実験用PCで,AVX2の命令が実行できるかを確かめます. Ubutu 22.04.4 LTS の場合,以下のコマンドで確認ができます.
$ grep -m 1 -e "^flags" /proc/cpuinfo -e avx2
flags : ...(略)... avx2 ...(略)...
AVX2 は 256 ビットごとの演算ができます. 倍精度浮動小数点数は 64 ビットなので,1つの拡張命令を, \(256/64=4\) 個のデータに同時に適用できます.
このようなCPUの拡張命令を利用する場合,演算対象の変数を格納するアドレスが,“キリのよい値” である必要があります. AVX2 の場合,そのアドレスは256ビット,つまり32バイトの倍数でなければなりません. このような,変数のアドレスに関する制約や,その制約に合わせて変数のメモリ上の格納位置を調整をすることを アライメント と呼びます.
C++ では, alignas キーワードでアライメント指定ができます.
例えば,
double a[const_val::kSize * const_val::kSize];
の代わりに,
alignas(32) double a[const_val::kSize * const_val::kSize];
とすることで,先頭アドレスが32バイトの倍数となるよう,変数がメモリ空間上に配置されます.
std::array<double, const_val::kSize * const_val::kSize> も同様に,以下のように指定できます.
alignas(32) std::array<doubl, const_val::kSize * const_val::kSize> a;
new でヒープ領域上にメモリを確保する方法や,std::vector を使う方法の場合,動的に確保した配列要素のアライメントを指定する手段はありそうですが,標準的な方法がわからなかったため,本ページでは省略します.
ここで,AVX2を使って,どのように行列積演算が効率化できるかを考えます.
\(C=AB\) とおきます. \(c^{[i,j]}=(c_{ij},c_{i+1,j},c_{i+2,j},c_{i+3,j})^T\) とします. ただし, \(\cdot^T\) は転置作用素です. このとき, \( \begin{aligned} c^{[i,j]}&=\begin{pmatrix}c_{ij}\\c_{i+1,j}\\c_{i+2,j}\\c_{i+3,j}\end{pmatrix}\\ &=\begin{pmatrix}\sum_{k=0}^{n-1}a_{ik}b_{kj}\\\sum_{k=0}^{n-1}a_{i+1,k}b_{kj}\\\sum_{k=0}^{n-1}a_{i+2,k}b_{kj}\\\sum_{k=0}^{n-1}a_{i+3,k}b_{kj}\end{pmatrix}\\ &=\sum_{k=0}^{n-1}b_{kj}\begin{pmatrix}a_{ik}\\a_{i+1,k}\\a_{i+2,k}\\a_{i+3,k}\end{pmatrix}\\ &=\sum_{k=0}^{n-1}\left(\begin{pmatrix}a_{ik}\\a_{i+1,k}\\a_{i+2,k}\\a_{i+3,k}\end{pmatrix}\odot(\bm{1}_4b_{kj})\right)\\ \end{aligned} \) と表せます. ただし, \(\bm{1}_4=(1,1,1,1)^T\) , \(x\odot y\) は要素ごとの積をとる演算を表します. \(c^{[i,j]}\,(i=0,4,8,\dots,n-4,\,j=0,1,\dots,n-1)\) を計算すると \(C\) のすべての要素が計算できることになりますので,以下の3つの演算が1つの拡張命令で実現できれば, \(c^{[i,j]}\) は効率的に計算できそうです.
- \(b_{kj}\mapsto \bm{1}_4b_{kj}\)
- \(\left(\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix},\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\right)\mapsto \begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}\odot\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\)
- \(\left(\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix},\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\right)\mapsto \begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}+\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}\)
Intel(R) Intrinsics Guide [1] によると,これらは,_mm256_broadcast_sd, _mm256_mul_pd, _mm256_add_pd で実現できることがわかります.
これら,AVX2で演算するために要素を読み込む _mm256_load_pd と, 演算結果を指定のアドレスに書き出す _mm256_store_pd をあわせると,AVX2 を用いた行列積演算の実装ができるようになります.
例えば,AVX2を使わない実装が以下のとおりであるとします (sdim_raw_array).
for (unsigned int i = 0; i < const_val::kSize; i++) {
for (unsigned int j = 0; j < const_val::kSize; j++) {
double& cij = c_[i + const_val::kSize*j];
for (unsigned int k = 0; k < const_val::kSize; k++) {
cij += a_[i + const_val::kSize*k] * b_[k + const_val::kSize*j];
}
}
}
これを,AVX2 を利用した実装に変更すると,以下のようになります (sdim_raw_array_avx).
constexpr std::size_t kSkipNumIndices = 256 / 64;
for (unsigned int i = 0; i < const_val::kSize; i += kSkipNumIndices) {
for (unsigned int j = 0; j < const_val::kSize; j++) {
__m256d added = _mm256_load_pd(&c_[i + const_val::kSize*j]);
for (unsigned int k = 0; k < const_val::kSize; k++) {
__m256d broadcast_b = _mm256_broadcast_sd(&b_[k + const_val::kSize*j]);
__m256d loaded_a = _mm256_load_pd(&a_[i + const_val::kSize*k]);
__m256d multiplied = _mm256_mul_pd(loaded_a, broadcast_b);
added = _mm256_add_pd(added, multiplied);
}
_mm256_store_pd(&c_[i + const_val::kSize*j], added);
}
}
ループ展開の利用 #
ところで,ループ展開という手法を使うと,さらに実行時間の短縮を図ることができます. 単にループで実現していた部分をベタ書きすることで,不要な処理が削減され,実行時間が短縮される場合があります.
4回展開する場合の実装例は以下の通りです (sdim_raw_array_avx_unroll).
単に4回分のループをベタ書きしているだけです.
constexpr std::size_t kSkipNumIndices = 256 / 64;
constexpr std::size_t kUnroll = 4;
for (unsigned int i = 0; i < const_val::kSize; i += kSkipNumIndices*kUnroll) {
for (unsigned int j = 0; j < const_val::kSize; j++) {
__m256d added0 = _mm256_load_pd(&c_[i + const_val::kSize*j]);
__m256d added1 = _mm256_load_pd(&c_[i + kSkipNumIndices + const_val::kSize*j]);
__m256d added2 = _mm256_load_pd(&c_[i + kSkipNumIndices*2 + const_val::kSize*j]);
__m256d added3 = _mm256_load_pd(&c_[i + kSkipNumIndices*3 + const_val::kSize*j]);
for (unsigned int k = 0; k < const_val::kSize; k++) {
__m256d broadcast_b = _mm256_broadcast_sd(&b_[k + const_val::kSize*j]);
__m256d loaded_a = _mm256_load_pd(&a_[i + const_val::kSize*k]);
__m256d multiplied = _mm256_mul_pd(loaded_a, broadcast_b);
added0 = _mm256_add_pd(added0, multiplied);
loaded_a = _mm256_load_pd(&a_[i + kSkipNumIndices + const_val::kSize*k]);
multiplied = _mm256_mul_pd(loaded_a, broadcast_b);
added1 = _mm256_add_pd(added1, multiplied);
loaded_a = _mm256_load_pd(&a_[i + kSkipNumIndices*2 + const_val::kSize*k]);
multiplied = _mm256_mul_pd(loaded_a, broadcast_b);
added2 = _mm256_add_pd(added2, multiplied);
loaded_a = _mm256_load_pd(&a_[i + kSkipNumIndices*3 + const_val::kSize*k]);
multiplied = _mm256_mul_pd(loaded_a, broadcast_b);
added3 = _mm256_add_pd(added3, multiplied);
}
_mm256_store_pd(&c_[i + const_val::kSize*j], added0);
_mm256_store_pd(&c_[i + kSkipNumIndices + const_val::kSize*j], added1);
_mm256_store_pd(&c_[i + kSkipNumIndices*2 + const_val::kSize*j], added2);
_mm256_store_pd(&c_[i + kSkipNumIndices*3 + const_val::kSize*j], added3);
}
}
数値実験 #
生の1次元配列と std::array による1次元配列による,以下の合計6種類の方法について,前ページまでと同様の方針で,実行時間を比較します.
- AVX2を使わない実装 (
sdim_raw_array,sdim_std_array) - AVX2を使う実装 (
sdim_raw_array_avx,sdim_std_array_avx) - AVX2を使って4回ループ展開もする実装 (
sdim_raw_array_avx_unroll,sdim_std_array_avx_unroll)
以下に計測条件を再掲します.
実行時間は,以下の手順で計測します.
- 行列積の演算を続けて10回行い,その開始時刻と終了時刻の差を10で割る.
- その操作を100回行い,その平均値を計測結果として採用する.
実行環境は以下のとおりです.
- CPU: 13th Gen Intel(R) Core(TM) i7-1360P (16コア)
- メモリ: 16.0GiB
- OS: Linux (Ubuntu 22.04.3 LTS)
- コンパイラ: g++ (Ubuntu 11.4.0-1ubuntu1~22.04) 11.4.0
実験結果は以下のとおりです.
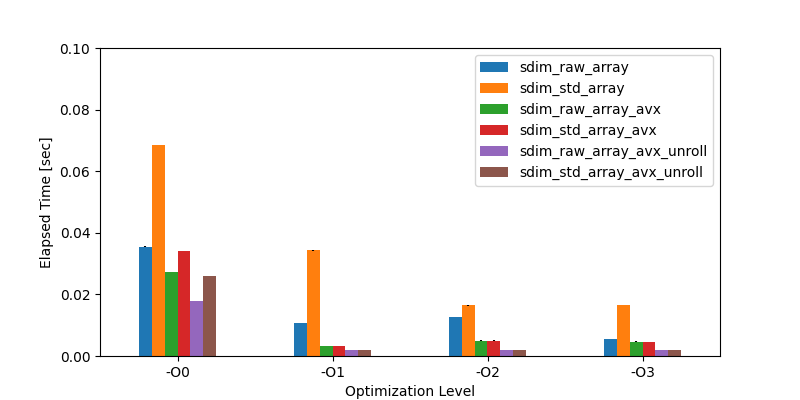
Figure 1. 実行結果
| Elapsed Time [sec] | -O0 | -O1 | -O2 | -O3 |
|---|---|---|---|---|
| sdim_raw_array | 0.035528 | 0.010755 | 0.012693 | 0.005464 |
| sdim_std_array | 0.068458 | 0.034348 | 0.016420 | 0.016439 |
| sdim_raw_array_avx | 0.027181 | 0.003242 | 0.005019 | 0.004688 |
| sdim_std_array_avx | 0.034000 | 0.003193 | 0.005014 | 0.004673 |
| sdim_raw_array_avx_unroll | 0.017972 | 0.001828 | 0.002041 | 0.002026 |
| sdim_std_array_avx_unroll | 0.026068 | 0.001836 | 0.001985 | 0.001985 |
最適化レベル1以上をみると,AVX2を使うと約3ミリ秒(約0.003秒),ループ展開まで使うと約2ミリ秒(約0.002秒)まで実行時間が短縮できていることがわかります.
特に,ループ展開によって実行時間がさらに短くなっていることもわかります.
最も実行時間が短かったのは,最適化レベル1の sdim_raw_array_avx_unroll の 0.001828 秒ですが,同じく最適化レベル1の sdim_raw_array は 0.010755 秒なので,AVX2 とループ展開の利用で,約 1/6 まで短縮できていることがわかります.
まとめ #
本ページでは,Intel CPU の拡張命令を用いて,行列積演算の実行時間が短縮できることを確認しました.
その結果,生の1次元配列で表現する方式 (sdim_raw_array) に AVX2 およびループ展開を利用すると,そうしない場合の約1/6の実行時間となり,ほぼ2ミリ秒(0.001828 秒)まで実行時間が短縮されたことがわかりました.
したがって,Intel CPU の拡張命令を用いた,SIMDによる実行時間の短縮効果が観測できたといえます.
AVX512 やその他のCPU拡張命令による,実行時間の短縮効果の確認は今後の課題です.
参考文献 #
[1] Intel,“Intel(R) Intrinsics Guide”, https://www.intel.com/content/www/us/en/docs/intrinsics-guide/index.html, 2024/7/5 最終アクセス.